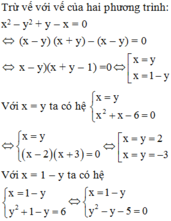tìm nghiệm nguyên của phương trình x2y2-x2-6y2=2xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
0
AH
Akai Haruma
Giáo viên
29 tháng 1 2023
Lời giải:
$x^2+4y^2-2xy=13$
$\Leftrightarrow (x^2+y^2-2xy)+3y^2=13$
$\Leftrightarrow (x-y)^2+3y^2=13$
$\Rightarrow 3y^2=13-(x-y)^2\leq 13< 15$
$\Rightarrow y^2< 5$
Vì $y^2\geq 0$ với mọi $y$ nguyên nên $y^2\in\left\{0; 1;4\right\}$
Với $y^2=0$:
$(x-y)^2=13-3y^2=13$ (loại vì 13 không là scp)
Với $y^2=1$:
$(x-y)^2=13-3y^2=10$ (loại vì 10 không là scp)
Với $y^2=4$:
$(x-y)^2=13-3y^2=1$
$\Rightarrow x-y=\pm 1$
$\Rightarrow x=y\pm 1$
$y^2=4\Rightarrow y=\pm 2$
Với $y=2$ thì $x=1$ hoặc $x=3$
Với $y=-2$ thì $x=-3$ hoặc $y=-1$
NS
0
PH
0
PT
1
PT
1
PT
1
CM
10 tháng 4 2019
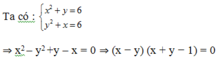
- Khi x = y thì x 2 + x - 6 = 0 ⇔ x = - 3 ; x = 2
- Khi y = 1 - x thì x 2 + 1 - x - 6 = 0 ⇔ x 2 - x - 5 = 0 ⇔ x 1 , 2 = 1 ± 21 2
Vậy hệ phương trình đã cho có 4 nghiệm (−3; −3), (2; 2), 1 + 21 2 ; 1 − 21 2 và 1 − 21 2 ; 1 + 21 2
Đáp án cần chọn là: B
