tìm số có 2 chữ số biết nếu chia số đó với tổng 2 chữ số ta đượcthuong là 7.Nếu đem tích 2 chữ số cộng 18 sẽ được số đó dảo lại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2019
Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
'
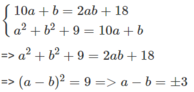Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.
LM
7 tháng 4 2020
Gọi số có 2 chữ số cần tìm là: ab \(\left(a,b\inℕ^∗;a,b\le9\right)\)
Theo bài ra, ta có hệ phương trình: \(\hept{\begin{cases}\overline{ab}
=6\left(a+b\right)\\\overline{ba}
=a.b+25\end{cases}
\Leftrightarrow\hept{\begin{cases}10a+b=6a+6b\\10b+a=ab+25\end{cases}
}}\)
\(\Leftrightarrow\hept{\begin{cases}4a=5b\\10b+a=a.b+25\end{cases}}
\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\9a=\frac{4a^2}{5}+25\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\4a^2-45a+125=0\end{cases}
\Leftrightarrow\hept{\begin{cases}b=\frac{4a}{5}\\\orbr{\begin{cases}a=5\\a=\frac{25}{4}
\left(loai\right)\end{cases}}\end{cases}}}
\Leftrightarrow\hept{\begin{cases}a=5\\b=4\end{cases}
}\)Vậy: số cần tìm là 54.
LM
7 tháng 4 2020
Ôi :(( Bạn tự giải nốt hệ phương trình và loại nghiệm phân số đi nhé :(( Không hiểu sao của mình bị mất 2 bước cuối :(( Xin lỗi bạn
26 tháng 10 2022
| có cái nịt |
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
BT
5 tháng 5 2017
Gọi số cần tìm có dạng: \(\overline{ab}\) \(\left(a,b\in N;a,b>0\right)\)
Thương của số cần tìm với tích hai chữ số của nó có dạng:\(\overline{ab}:\left(ab\right)\).
Theo giả thiết ta có: \(\overline{ab}=2ab+18\).
Tổng bình phương các chữ số của số cần tìm là: \(a^2+b^2+9=\overline{ab}\).
Ta có hệ phương trình: \(\left\{{}\begin{matrix}2ab+18=\overline{ab}\\a^2+b^2+9=\overline{ab}\end{matrix}\right.\)\(\Rightarrow a^2+b^2+9=2ab+18\)\(\Leftrightarrow\left(a-b\right)^2=9\)\(\Leftrightarrow\left|a-b\right|=3\).
Th 1. \(a-b=3\)\(\Leftrightarrow a=b+3\). Khi đó:
\(2ab+18=\overline{ab}\)\(\Leftrightarrow2ab+18=10a+b\)\(\Leftrightarrow2\left(b+3\right)b+18=10\left(b+3\right)+b\)\(\Leftrightarrow2b^2-5b-12=0\)\(\Leftrightarrow\left\{{}\begin{matrix}b=4\left(tm\right)\\b=\dfrac{-3}{2}\left(l\right)\end{matrix}\right.\).
Với \(b=4\) ta có \(a=3+b=3+4=7\). Vậy số đó là 73.
Th2: \(a-b=-3\)\(\Leftrightarrow a=b-3\). Khi đó:
\(2ab+18=10a+b\)\(\Leftrightarrow2\left(b-3\right)b+18=10\left(b-3\right)+b\)
\(\Leftrightarrow2b^2-17b+48=0\) (Vô nghiệm).
Vậy số cần tìm là: 73.
27 tháng 10 2016
Gọi số cần tìm là ab ( a;b < 10)
Theo bài ra ta có :
ab +(a+b)=83
a*10+b+a+b=83
a*11+b*2=83
-Nếu a=8 thì a*11=88
=> a<8
-Nếu a=5 và b có giá trị lớn nhất bằng 9 thì a*11+b*2=5*11+9*2=73
=> a>5
Vậy a = 6 hoặc 7
-Nếu a=6 thì a*11+b*2 = 6*11+b*2
6*11+b*2 = 83
66+b*2 = 83
b*2 = 83-66
b*2 = 17 ( loại vì không thể tìm được b )
- Nếu a=7 thì a*11 +b*2 = 7*11 + b*2
77+b*2 = 83
b*2 = 83-77
b*2 = 6
b = 6/2
b = 3
Vậy số cần tìm là 73
gọi số có 2 chữ số phải tìm là : \(\overline{ab}\left(a;b\in z;a\ne0\right)\)
vì nếu chia số đó cho tổng 2 chữ số ta được thương là 7 nên ta có phương trình: \(\overline{ab}=\left(a+b\right)7\) \(\Leftrightarrow10a+b=7a+7b\)
\(\Leftrightarrow3a=6b\Leftrightarrow a=2b\left(1\right)\)
vì nếu đem tích 2 chữ số cộng 18 sẽ được số nghịch đảo số đo nên ta có phương trình: ab+18=\(\overline{ba}\)
\(\Leftrightarrow10b+a=ab+18\left(2\right)\)
từ(1) và(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a=2b\\10b+a=ab+18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2b\\12b=2b^2+18\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\b^2-6b+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\\left(b-3\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\a=6\end{matrix}\right.\) (tm)
vậy số có 2 chữ số phải tìm là: 63