Cách làm bài này ạ??????
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 3 2022
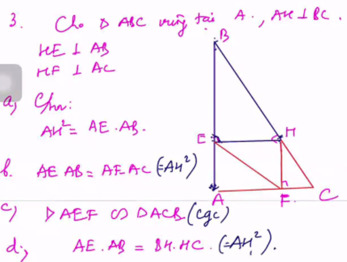
tất cả các ý mình cm thành cụm luôn nhé
Xét tam giác AHE và tam giác ABH ta có
^A _ chung
^AHE = ABH = 900
Vậy tam giác AHE ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AE}{AH}\Rightarrow AH^2=AE.AB\)(1)
Xét tam giác AHC và tam giác AFH có
^A _ chung
^AHC = ^AFH = 900
Vậy tam giác AHC ~ tam giác AFH (g.g)
\(\dfrac{AH}{AF}=\dfrac{AC}{AH}\Rightarrow AH^2=AF.AC\)(2)
Từ (1) ; (2) suy ra \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(*)
Xét tam giác AEF và tam giác ABC có
^A _ chung ; có (*)
Vậy tam giác AEF ~ tam giác ABC (c.g.c)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 3 2023
Ta có:
\(\dfrac{ab+bc+ca}{2\left(a^2+b^2+c^2\right)}+\dfrac{1}{6}\left(\dfrac{a^2+b^2+c^2}{abc}\right)\ge2\sqrt{\dfrac{1}{12}\left(\dfrac{ab+ca+ca}{abc}\right)}=\sqrt{3\left(\dfrac{ab+bc+ca}{abc}\right)}\)
Nên ta chỉ cần cm:
\(\sqrt{\dfrac{1}{3}\left(\dfrac{ab+bc+ca}{abc}\right)}\ge\dfrac{a+b+c}{3}\Leftrightarrow3\left(\dfrac{ab+bc+ca}{abc}\right)\ge\left(a+b+c\right)^2\)
Thật vậy, ta có:
\(\dfrac{3\left(ab+bc+ca\right)}{abc}=\dfrac{\left(a^2b+b^2c+c^2a\right)\left(ab+bc+ca\right)}{abc}\)
\(=\left(\dfrac{a}{c}+\dfrac{b}{a}+\dfrac{c}{b}\right)\left(ac+ab+bc\right)\ge\left(a+b+c\right)^2\) (Bunhiacopxki)
Dấu "=" xảy ra khi \(a=b=c=1\)
KV
3 tháng 4 2022
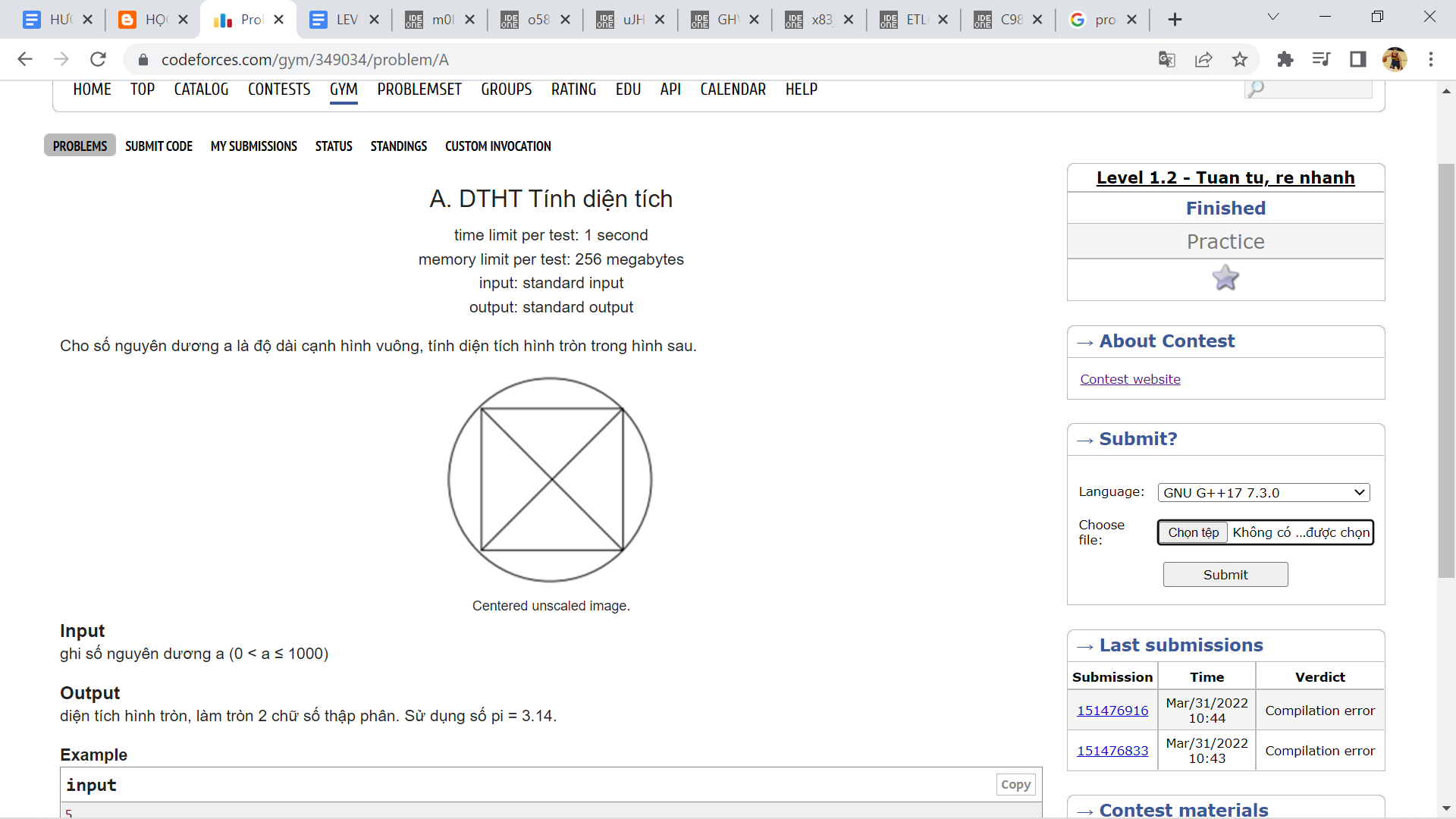
Var a, s:real;
Begin
Write('Nhap a = ');readln(a);
S:=3.14*a*a/2;
Write('Dien tich hinh tron la ',s:10:2);
Readln;
End.
CT
0
T
1
12 tháng 12 2021
\(\dfrac{x+1}{2x^2-x^4}=\dfrac{x+1}{x^2\left(2-x^2\right)}=\dfrac{-\left(x+1\right)\left(x^4+2x^2+4\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{x}{x^4+2x^2+4}=\dfrac{x^3\left(x^2-2\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\\ \dfrac{2x-1}{x^7-8x}=\dfrac{2x-1}{x\left(x^6-8\right)}=\dfrac{x\left(2x-1\right)}{x^2\left(x^2-2\right)\left(x^4+2x^2+4\right)}\)
E
0
L
1
KN
4 tháng 10 2019
\(\left|2x-1\right|=\left|2x+3\right|\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=2x+3\\2x-1=-2x-3\end{cases}}\Leftrightarrow\orbr{\begin{cases}0=4\left(L\right)\\4x=-2\end{cases}}\Leftrightarrow x=\frac{-1}{2}\)
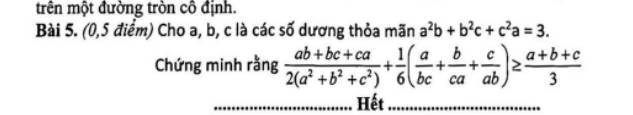
Giải hộ câu này ạ
\(\dfrac{x^4-25+2x^3+10x}{x^2+5}\)
\(=\dfrac{\left(x^2-5\right)\left(x^2+5\right)+2x\left(x^2+5\right)}{x^2+5}\)
\(=x^2+2x-5\)