giúp mik với cảm ơn mn nhiều ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CT
1
Những câu hỏi liên quan
9 tháng 11 2021
Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)
LT
1
27 tháng 3 2022
a) Xét \(\Delta BAD\) và \(\Delta BCE:\)
\(\widehat{B}chung.\)
\(\widehat{D}=\widehat{E}\left(=90^o\right).\)
\(\Rightarrow\Delta BAD\sim\Delta BCE\left(g-g\right).\)
b) Xét \(\Delta ABC:\)
CE là đường cao \(\left(CE\perp AB\right).\)
AD là đường cao \(\left(AD\perp BC\right).\)
Mà F là giao điểm của CE và AD.
\(\Rightarrow BF\) là đường cao.
Xét \(\Delta ABC\) cân tại B:
BF là đường cao (gt).
\(\Rightarrow BF\) là phân giác \(\widehat{ABC}.\)
HN
1
8 tháng 3 2022
\(=\left(\dfrac{1}{49}-\dfrac{1}{9}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{49^2}\right)=0\)
NA
1
2 tháng 3 2023
Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
P
2
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Bạn cần hỗ trợ bài nào thì nên chụp nguyên bài đó ra thôi. Nếu bạn cần giúp nhiều bài thì nên tách lẻ mỗi bài mỗi post hoặc 2 bài/ post. Bạn chụp như thế này gây "ngợp" nên sẽ ít ai dừng lại và hỗ trợ.
LP
1
4 tháng 9 2021
a: \(x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
b: \(27y^3+1=\left(3y+1\right)\left(9y^2-3y+1\right)\)
c: \(x^3-27=\left(x-3\right)\left(x^2+3x+9\right)\)
d: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
e: \(8x^3+1=\left(2x+1\right)\left(4x^2-2x+1\right)\)
f: \(27x^3+64y^3=\left(3x+4y\right)\left(9x^2-12xy+16y^2\right)\)
g: \(x^3-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
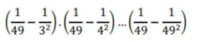
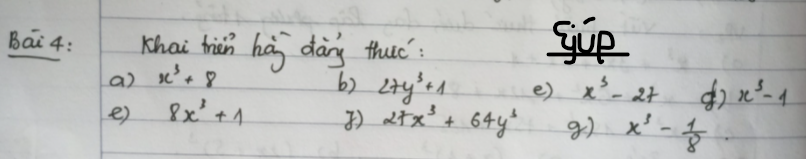
smoothly - competitive - disappointing - apology - representative - finally
một cách trơn tru - mang tính cạnh tranh - đáng thất vọng - lời xin lỗi - người đại diện - cuối cùng