1+2+3+1
1+2+3+1
1+2+3+1=......
Bài toán này đã học ở tiểu học
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hiệu giữa số hs giải toán Violympic và số hs giải toán tuổi thơ là số có 2 chữ số ta gọi là \(\overline{ab}\)
\(\overline{ab}\) chia 5 dư 2 => b=2 hoặc b=7
+ Với \(b=2\Rightarrow\overline{ab}=\overline{a2}\Rightarrow\overline{a2}-2⋮9\Rightarrow10xa+2-2=10xa⋮9\Rightarrow a=9\)
\(\Rightarrow\overline{ab}=92\)
+ Với \(b=7\Rightarrow\overline{ab}=\overline{a7}\Rightarrow\overline{a7}-2⋮9\Rightarrow10xa+7-2=10xa+5⋮9\Rightarrow a=4\)
\(\Rightarrow\overline{ab}=47\)
Ta có
3/11 số hs giải toán tuổi thơ = 5/19 số hs giải toán Vio
=> 15/55 số hs giải toán tuổi thơ = 15/57 số hs giải toán vio
=> 1/55 số hs giải toán tuổi thơ = 1/57 số hs giải toán vio
Chia số hs giải toán tuổi thơ thành 55 phần thì số hs giải toán vio là 57 phần
Hiệu số phần bằng nhau là
57-55=2 phần
Như vậy hiệu số hs giải 2 loại toán phải là 1 số chia hết cho 2 tức là 1 số chẵn. Vì vậy hiệu số hs giải 2 loại toán là 92
Giá trị 1 phần là
92:2=46 em
Số hs giải toán tuổi thơ là
46x55=2530 hs
Số hs giải toán vio là
46x57=2622 hs

Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
![]()
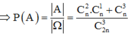
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2

1. Bài giải
Số học sinh nam của trường tiểu học đó là
902-345=557(học sinh nam )
Số học sinh nữ ít hơn số học sinh nam là số học sinh là
557-345=212(học sinh)
Đáp số 212 học sinh
2.345-200=145
3.340+200=540

Bài này mình không tính nhanh được, còn nếu tính bình thường thì:
Chắc bạn đã biết cách tính tổng của dãy số cách đều, ta có: \(1+2+3+...+n=\frac{n\left(n+1\right)}{2}\)
Do đó tổng cần tìm của bạn là:
\(S=\frac{1}{1+2}+\frac{1}{1+2+3}+\frac{1}{1+2+3+4}+...+\frac{1}{1+2+3+4+...+50}\)
\(S=\frac{1}{\frac{2\cdot3}{2}}+\frac{1}{\frac{3\cdot4}{2}}+\frac{1}{\frac{4\cdot5}{2}}+...+\frac{1}{\frac{50\cdot51}{2}}=\frac{2}{2\cdot3}+\frac{2}{3\cdot4}+\frac{2}{4\cdot5}+...+\frac{2}{50\cdot51}\)
Vậy, \(\frac{1}{2}S=\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{50\cdot51}\)
\(\frac{1}{2}S=\frac{3-2}{2\cdot3}+\frac{4-3}{3\cdot4}+\frac{5-4}{4\cdot5}+...+\frac{51-50}{50\cdot51}\)
\(\frac{1}{2}S=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{50}-\frac{1}{51}=\frac{1}{2}-\frac{1}{51}=\frac{51-2}{2\cdot51}=\frac{49}{2\cdot51}\)
Vậy \(S=\frac{49}{51}\)
Bài này chắc không phải lớp 4 nhé bạn!