Giải các phương trình sau:
a, x4 + 3x2 + 9 = 0
b, x4 + 5x2 + 9 = 0
c, x4 - 3x2 + 9 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 7 2019
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
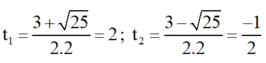
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
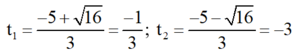
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
CM
7 tháng 7 2019
Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm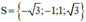 
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
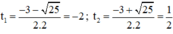
t 1 = - 2 < 0 nên loại.
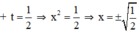
Vậy phương trình có tập nghiệm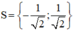 
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
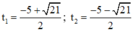
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
a.
\(x^3-7x+6=0\)
\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)
\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
f.
\(x^4-4x^3+12x-9=0\)
\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)
\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)
CM
14 tháng 4 2017
a) Ta có: Δ = 196 > 0
Phương trình có 2 nghiệm x 1 = 3 , x 2 = 1 5
b) Đặt t = x 2 , t ≥ 0 , phương trình trở thành t 2 + 9 t − 10 = 0
Giải ra được t=1 (nhận); t= -10 (loại)
Khi t=1, ta có x 2 = 1 ⇔ x = ± 1 .
c) 3 x − 2 y = 10 x + 3 y = 7 ⇔ 3 x − 2 y = 10 ( 1 ) 3 x + 9 y = 21 ( 2 )
(1) – (2) từng vế ta được: y=1
Thay y= 1 vào (1) ta được x= 4
Vậy hệ phương trình có nghiệm duy nhất là x= 4; y= 1.
DT
Đỗ Thanh Hải
CTVVIP
16 tháng 4 2021
1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
Vậy hpt có nghiệm (x;y) = (3;4)
2)
a) 3x2 - 2x - 1 = 0
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Vậy pt có nghiệm x = 1 hoặc x = 3
b) Đặt x2 = t (t \(\ge\) 0)
Pt trở thành: t2 - 20t + 4 = 0
\(\Delta\) = (-20)2 - 4.1.4 = 400 - 16 = 384
=> pt có 2 nghiệm phân biệt t1 = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)
t2 = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)
=> x1 = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)
x2 = \(2-\sqrt{6}\)
LT
15 tháng 4 2021
a) \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14y=-42\\2x+3y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
b) \(3x^2+4x=0\)
\(\Leftrightarrow x\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{0;-\dfrac{4}{3}\right\}\)
c) Đặt: \(x^2=t\left(t\ge0\right)\)
\(\Rightarrow\) Ta có phương trình mới:
\(t^2-3t-4=0\)
Ta có: a - b + c = 1 + 3 - 4 = 0
\(\Rightarrow t_1=-1\left(loại\right);t_2=4\left(TM\right)\)
\(\Rightarrow x=\pm2\)
Vậy tập nghiệm của phương trình là: S = {2; -2}
15 tháng 4 2021
a, \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\left(1\right)\\6x-5y=27\left(2\right)\end{matrix}\right.\)
Lấy (1) - (2) ta được : \(14y=-15-27=-42\Leftrightarrow y=-3\)
\(\Rightarrow6x-27=-15\Leftrightarrow6x=12\Leftrightarrow x=2\)
Vậy \(\left(x;y\right)=\left(2;-3\right)\)
b, \(3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow x=0;x=-\dfrac{4}{3}\)
c, \(x^4-3x^2-4=0\Leftrightarrow x^4+x^2-4x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x^2-4=0\Leftrightarrow\left(x^2+1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow x=\pm2;x^2+1>0\)
Vậy nghiệm của phương trình là x = -2 ; x = 2
VM
20 tháng 3 2022
a, Có \(\left(x^2-9\right)^2\)≥0 ∀ x ∈ Z
|y-2| ≥0 ∀ y ∈ Z
⇒ Gía trị nhỏ nhất A=-1. Dấu ''='' xảy ra khi:\(\left(x^2-9\right)^2\)+|y-2|=0
⇒ \(x=3\) ; \(y=2\)
Vậy.....
b, Có \(x^4\) ≥ 0 ∀ x ∈ Z
3\(x^2\) ≥ 0 ∀ x ∈ Z
⇒ Giá trị nhỏ nhất của B=2. Dấu ''='' xảy ra khi: \(x^4\)+3\(x^2\)=0
⇒ \(x^2\left(x^2+3\right)\)=0
⇒ \(x^2\) =0
⇒ \(x=0\)
Vậy...
CM
4 tháng 11 2017
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
AH
Akai Haruma
Giáo viên
24 tháng 8 2021
a.
$x^4-25x^3=0$
$\Leftrightarrow x^3(x-25)=0$
\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)
b.
$(x-5)^2-(3x-2)^2=0$
$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$
$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix}
-2x-3=0\\
4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix}
x=\frac{-3}{2}\\
x=\frac{7}{4}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
24 tháng 8 2021
c.
$x^3-4x^2-9x+36=0$
$\Leftrightarrow x^2(x-4)-9(x-4)=0$
$\Leftrightarrow (x-4)(x^2-9)=0$
$\Leftrightarrow (x-4)(x-3)(x+3)=0$
\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)
d. ĐK: $x\neq 0$
$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$
$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$
$\Leftrightarrow -2(-x^2+3x-4)=0$
$\Leftrightarrow x^2-3x+4=0$
$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)
Vậy pt vô nghiệm.
2 tháng 9 2021
Bài 2:
a) \(3x^2-7x-10=\left(x+1\right)\left(3x-10\right)\)
b) \(x^2+6x+9-4y^2=\left(x+3\right)^2-\left(2y\right)^2=\left(x+3-2y\right)\left(x+3+2y\right)\)
c) \(x^2-2xy+y^2-5x+5y=\left(x-y\right)^2-5\left(x-y\right)=\left(x-y\right)\left(x-y-5\right)\)
d) \(4x^2-y^2-6x+3y=\left(2x-y\right)\left(2x+y\right)-3\left(2x-y\right)=\left(2x-y\right)\left(2x+y-3\right)\)
e) \(1-2a+2bc+a^2-b^2-c^2=\left(a-1\right)^2-\left(b-c\right)^2=\left(a-1-b+c\right)\left(a-1+b-c\right)\)
f) \(x^3-3x^2-4x+12=\left(x+2\right)\left(x-3\right)\left(x-2\right)\)
g) \(x^4+64=\left(x^2+8\right)^2-16x^2=\left(x^2+8-4x\right)\left(x^2+6+4x\right)\)h) \(x^4-5x^2+4=\left(x+2\right)\left(x+1\right)\left(x-1\right)\left(x-2\right)\)
i) \(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+16=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+16=\left(x^2+8x+7\right)^2+8\left(x^2+8x+7\right)+16=\left(x^2+8x+11\right)^2\)
2 tháng 9 2021
a: \(3x^2-7x-10\)
\(=3x^2+3x-10x-10\)
\(=\left(x+1\right)\left(3x-10\right)\)
b: \(x^2+6x+9-4y^2\)
\(=\left(x+3\right)^2-4y^2\)
\(=\left(x+3-2y\right)\left(x+3+2y\right)\)
c: \(x^2-2xy+y^2-5x+5y\)
\(=\left(x-y\right)^2-5\left(x-y\right)\)
\(=\left(x-y\right)\left(x-y-5\right)\)
a) \(x^4+3x^2+9=0\)
\(\Leftrightarrow\left(x^2\right)^2+2\cdot x^2\cdot\frac{3}{2}+\left(\frac{3}{2}\right)^2+\frac{27}{4}=0\)
\(\Leftrightarrow\left(x^2+\frac{3}{2}\right)^2=-\frac{27}{4}\) ( vô nghiệm do \(\left(x^2+\frac{3}{2}\right)^2\ge0\ne-\frac{27}{4}\forall x\))
b) \(x^4+5x^2+9=0\)
\(\Leftrightarrow\left(x^2\right)^2+2\cdot x^2\cdot\frac{5}{2}+\left(\frac{5}{2}\right)^2+\frac{11}{4}=0\)
\(\Leftrightarrow\left(x^2+\frac{5}{2}\right)^2=-\frac{11}{4}\) ( vô nghiệm do \(\left(x^2+\frac{5}{2}\right)^2\ge0\ne-\frac{11}{4}\forall x\) )
c) \(x^4-3x^2+9=0\)
\(\Leftrightarrow\left(x^2\right)^2-2\cdot x^2\cdot\frac{3}{2}+\left(\frac{3}{2}\right)^2+\frac{27}{4}=0\)
\(\Leftrightarrow\left(x^2-\frac{3}{2}\right)^2=-\frac{27}{4}\) ( vô nghiệm do \(\left(x^2-\frac{3}{2}\right)^2\ge0\ne-\frac{27}{4}\forall x\) )
a) Đặt \(x^2=t\left(t\ge0\right)\)
Phương trình trở thành: \(t^2+3t+9=0\)
Ta có: \(\Delta=3^2-4.9=-27< 0\)
Vậy phương trình vô nghiệm
b) Đặt \(x^2=t\left(t\ge0\right)\)
Phương trình trở thành: \(t^2+5t+9=0\)
Ta có: \(\Delta=5^2-4.9=-11< 0\)
Vậy phương trình vô nghiệm
c) Đặt \(x^2=t\left(t\ge0\right)\)
Phương trình trở thành: \(t^2-3t+9=0\)
Ta có: \(\Delta=3^2-4.9=-27< 0\)
Vậy phương trình vô nghiệm