Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

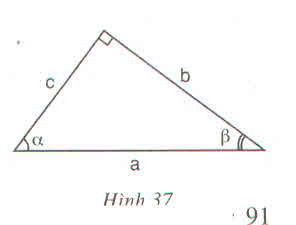
sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
a) b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC
b) b = c. (b/c) = c.tgB = c.cotgC
c = b.(c/b) = b.cotgB = b.tgC

sinB = b/a; cosB = c/a; tgB = b/c; cotgB = c/b
sinC = c/a; cosC = b/a; tgC = c/b; cotgB = b/c
b = a.(b/a) = a.sinB = a.cosC
c = a. (c/a) = a.cosB = a.sinC

a/ Kẻ đường cao AH => BH là hình chiếu của AB trên BC và CH là hình chiếu của AC trên BC
Giả sử \(\frac{AB}{AC}=k\Rightarrow\frac{AB^2}{AC^2}=k^2\)
Ta có \(AB^2=BH.BC;AC^2=CH.BC\Rightarrow\frac{AB^2}{AC^2}=\frac{BH}{CH}=k^2\)
b/ Áp dụng câu A sẽ tính được tỷ số hình chiếu 2 cạnh góc vuông trên BC là mà biết chiều dài BC=82 bài toán là dạng tìm 2 số khi biết tổng và tỷ ở lớp 5 rồi bạn tự giải nốt nhé