tìm m để hai đường thẳng (d1): 3x+my=3 và (d2): mx + 3y=3 song song với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để \(\left(d_1\right):3x+my=3\) và \(\left(d_2\right):mx+3y=3\) song song với nhau thì hệ phương trình \(\left\{{}\begin{matrix}3x+my=3\\mx+3y=3\end{matrix}\right.\) vô nghiệm.
Tức là \(\frac{3}{m}=\frac{m}{3}\ne\frac{3}{3}\) \(\Leftrightarrow m^2=9;m\ne3\)\(\Leftrightarrow m=-3\)
Vậy với m=-3 thì thỏa mãn ycbt
Ta có:
\(\left(d1\right)=3x+my=3\Leftrightarrow y=\frac{3}{m}x-\frac{3}{m}\)
\(\left(d2\right)=mx+3y=3\Leftrightarrow y=\frac{m}{3}x-1\)
Để d1 // d2 thì\(\left\{{}\begin{matrix}\frac{3}{m}=\frac{m}{3}\\\frac{-3}{m}\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2=9\\m\ne3\end{matrix}\right.\Leftrightarrow m=-3}}\)Vậy m=-3

\(d_1:mx+y=3m-1.\\ \Leftrightarrow-mx+3m-1=y.\)
\(d_2:x+my=m+1.\\ \Leftrightarrow my=-x+m+1.\\\Leftrightarrow y=\dfrac{-x}{m}+\dfrac{m}{m}+\dfrac{1}{m}.\Leftrightarrow y=-\dfrac{1}{m}x+1+\dfrac{1}{m}.\)
Thay m = 2 vào phương trình đường thẳng d1 ta có:
\(-2x+3.2-1=y.\\ \Leftrightarrow-2x+5=y.\)
Thay m = 2 vào phương trình đường thẳng d2 ta có:
\(y=-\dfrac{1}{2}x+1+\dfrac{1}{2}.\\ \Leftrightarrow y=\dfrac{-1}{2}x+\dfrac{3}{2}.\)
Xét phương trình hoành độ giao điểm của d1 và d2 ta có:
\(-2x+5=\dfrac{-1}{2}x+\dfrac{3}{2}.\\ \Leftrightarrow\dfrac{-3}{2}x=-\dfrac{7}{2}.\\ \Leftrightarrow x=\dfrac{7}{3}.\)
\(\Rightarrow y=\dfrac{1}{3}.\)
Tọa độ giao điểm của d1 và d2 khi m = 2 là \(\left(\dfrac{7}{3};\dfrac{1}{3}\right).\)

Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.

Để hai đường thẳng song song thì:
m 2 = 2 m − 2 3 ≠ − m + 6 1 ⇔ m 2 = 2 m − 2 3 m 2 ≠ − m + 6 1 ⇔ 3 m = 4 m − 4 m ≠ − 2 m + 12 ⇔ m = 4 m ≠ 4
không tồn tại m thỏa mãn yêu cầu bài toán.
ĐÁP ÁN D

Chọn C.
d1 song song với d2 khi và chỉ khi 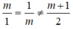 khi đó ta có:
khi đó ta có:
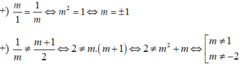
Vậy m = -1.

a: Để hai đường cắt nhau thì 1/m<>m/4
=>m2<>4
hay \(m\notin\left\{2;-2\right\}\)
b: Để hai đường song song thì 1/m=m/4
hay \(m\in\left\{2;-2\right\}\)
<=>\(\hept{\begin{cases}3=M\\M\ne3\end{cases}}\)
<=>\(\hept{\begin{cases}M=3\\M\ne3\end{cases}}\)
=> không có giá trị của M để d1\(//\)d2