Trong một hộp kín đựng 100 tấm thẻ như nhau được đánh số từ 1 tới 100. Lấy ngẫu nhiên ba tấm thẻ trong hộp. Tính xác suất lấy được 3 tấm thẻ mà số ghi trên 3 tấm thẻ đó lập thành :
a) Một cấp số cộng ?
b) Một cấp số nhân ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
15 tháng 9 2023
Gọi số thẻ ghi số lẻ trong hộp là \(n\). Khi đó, xác suất tấm thẻ lấy ra ghi số lẻ là \(\frac{n}{{10}}\).
Số thẻ ghi số chẵn trong hộp là \(10 - n\). Khi đó, xác suất tấm thẻ lấy ra ghi số chẵn là \(\frac{{10 - n}}{{10}}\).
Vì xác suất lấy được thẻ chẵn gấp 4 lần xác suất lấy được thẻ lẻ nên \(\frac{{10 - n}}{{10}} = 4.\frac{n}{{10}} \Leftrightarrow 10 - n = 4n \Leftrightarrow 5n = 10 \Leftrightarrow n = 2\)
Vậy số thẻ ghi số lẻ trong hộp là 2 thẻ.
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...
CM
4 tháng 6 2017
HD: Số phần tử của không gian mẫu là: Ω = C 11 4
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.
CM
10 tháng 11 2017
Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra
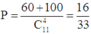
Ý tưởng khá đơn giản:
a/ Cấp số cộng thì \(a+c=2b\) nên a;c cùng tính chẵn lẻ, vậy chỉ cần tìm số cặp cùng tính chẵn lẻ
b/ Cấp số nhân thì \(a.q^2=c\), do đó chỉ cần tìm số bội số phân biệt của các số chính phương không lớn hơn 100