Cho tam giác ABC có AB = 15 cm, AC = 21 cm. Lấy hai điểm M, N lần lượt trên
hai cạnh AB, AC sao cho AM = 10 cm, AN = 14 cm. Chứng minh MN đi qua trọng tâm
của tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

14 tháng 2 2020
Cho AH là trung tuyến tgiac ABC, AH cắt MN tại O
Có \(\frac{AM}{AB}=\frac{10}{15}=\frac{2}{3},\frac{AN}{AC}=\frac{14}{21}=\frac{2}{3}\)
\(\Rightarrow\frac{AM}{AB}=\frac{AN}{AC}=\frac{2}{3}\Rightarrow\) MN//BC
Xét \(\Delta ABH\) có MO//BH \(\Rightarrow\frac{AM}{AB}=\frac{AO}{AH}=\frac{2}{3}\Rightarrow\) O là trọng tâm tgiac ABC đc MN đi qua

2 tháng 5 2021
a, theo pitago đảo: 212 +282=1225=352 suy ra tam giác ABC vuông
b,theo pitago
AH2=AB2-BH2=AC2-CH2 suy ra 2AH2=AB2+AC2-BH2-CH2
suy ra 2AH2=BC2-BH2-CH2 (Mà BC=BH+CH) suy ra 2AH2=2BHxCH

15 tháng 3 2022
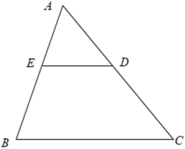
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC
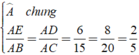
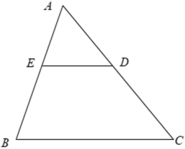
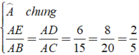
Xét \(\Delta\)AMN và \(\Delta\)ABC có:
\(\frac{AM}{AB}=\frac{AN}{AC}\left(\frac{10}{15}=\frac{14}{21}\right)\)
=> MN // BC (1)
Gọi M là trung điểm của BC.
Gọi G là giao điểm AM và MN
Xét \(\Delta\)ABM có:
MG// BM ( theo(1))
=> \(\frac{AG}{AM}=\frac{AM}{AB}=\frac{10}{15}=\frac{2}{3}\)
=> G là trọng tâm của \(\Delta\)ABC
Vậy MN qua trong tâm \(\Delta\)ABC.