bài này thì làm sao vậy mọi người
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1 chắc chắn sai vì pt d' ko cùng phương với d
Còn sai ở đâu thì nhìn cách làm rối loạn quá nên ko biết
Làm cách 1 theo kiểu "cơ bản" thì:
\(A\left(-1;1\right)\Rightarrow\left\{{}\begin{matrix}x_{A'}=-3.\left(-1\right)+\left(1-\left(-3\right)\right).\left(-1\right)=-1\\y_{A'}=-3.1+\left(1-\left(-3\right)\right).3=9\end{matrix}\right.\) \(\Rightarrow A'\left(-1;9\right)\)
\(B\left(2;-1\right)\Rightarrow\left\{{}\begin{matrix}x_{B'}=-3.2+\left(1-\left(-3\right)\right).\left(-1\right)=-10\\y_{B'}=-3.\left(-1\right)+\left(1-\left(-3\right)\right).3=15\end{matrix}\right.\) \(\Rightarrow B'\left(-10;15\right)\)
\(\Rightarrow\overrightarrow{A'B'}=\left(-9;6\right)=3\left(-3;2\right)\)
Phương trình A'B':
\(2\left(x+1\right)+3\left(y-9\right)=0\Leftrightarrow2x+3y-25=0\)

\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =1-\left(\dfrac{1}{2}-\dfrac{1}{2}\right)-\left(\dfrac{1}{3}-\dfrac{1}{4}\right)-...-\left(\dfrac{1}{99}-\dfrac{1}{99}\right)-\dfrac{1}{100}\\ =1-0-0-...-0-\dfrac{1}{100}\\ =1-\dfrac{1}{100}\\ =\dfrac{99}{100}\)
Tách thành hiệu 2 phân số đối với mỗi phân số
Kết quả: 1 - 1/100 = 99/100 = 0,99


Số hạng tử X:
(100 - 0): 2 + 1 = 51 (hạng tử)
Tổng hạng tử số:
(100+2) x (50:2)= 2550
Tổng của 51 hạng tử X:
2601 - 2550=51
X có giá trị bằng:
51:51=1
Vậy x=1
` @ L I N H `
Số hạng tử X:
(100 - 0): 2 + 1 = 51 (hạng tử)
Tổng hạng tử số:
(100+2) x (50:2)= 2550
Tổng của 51 hạng tử X:
2601 - 2550=51
X có giá trị bằng:
51:51=1
Vậy x=1


a/ \(F_{ms}=F_k\Leftrightarrow\mu mg=F_k=0,2.2.10=4\left(N\right)\)
b/ \(F_{ms}=-ma\Leftrightarrow a=-\dfrac{F_{ms}}{m}=-\mu g=-0,2.10=-2\left(m/s^2\right)\)
\(S=v_0t+\dfrac{1}{2}at^2=v_0t-t^2\)
Nếu đề bài ko sai thì v0=0 (m/s) thì thời gian đi hết bằng 0 sẽ nhỏ nhất thôi, bởi vì nhìn cái hàm kia là biết có 3 đại lượng S,v0 và t luôn liên hệ với nhau, thay đổi v0 thì sẽ dẫn đến thay đổi t (nếu coi S là const), nên tui nghĩ chỉ có thể là bằng 0 thôi. Bạn thử lên xem giáo viên nói thế nào đi về cta bàn tiếp





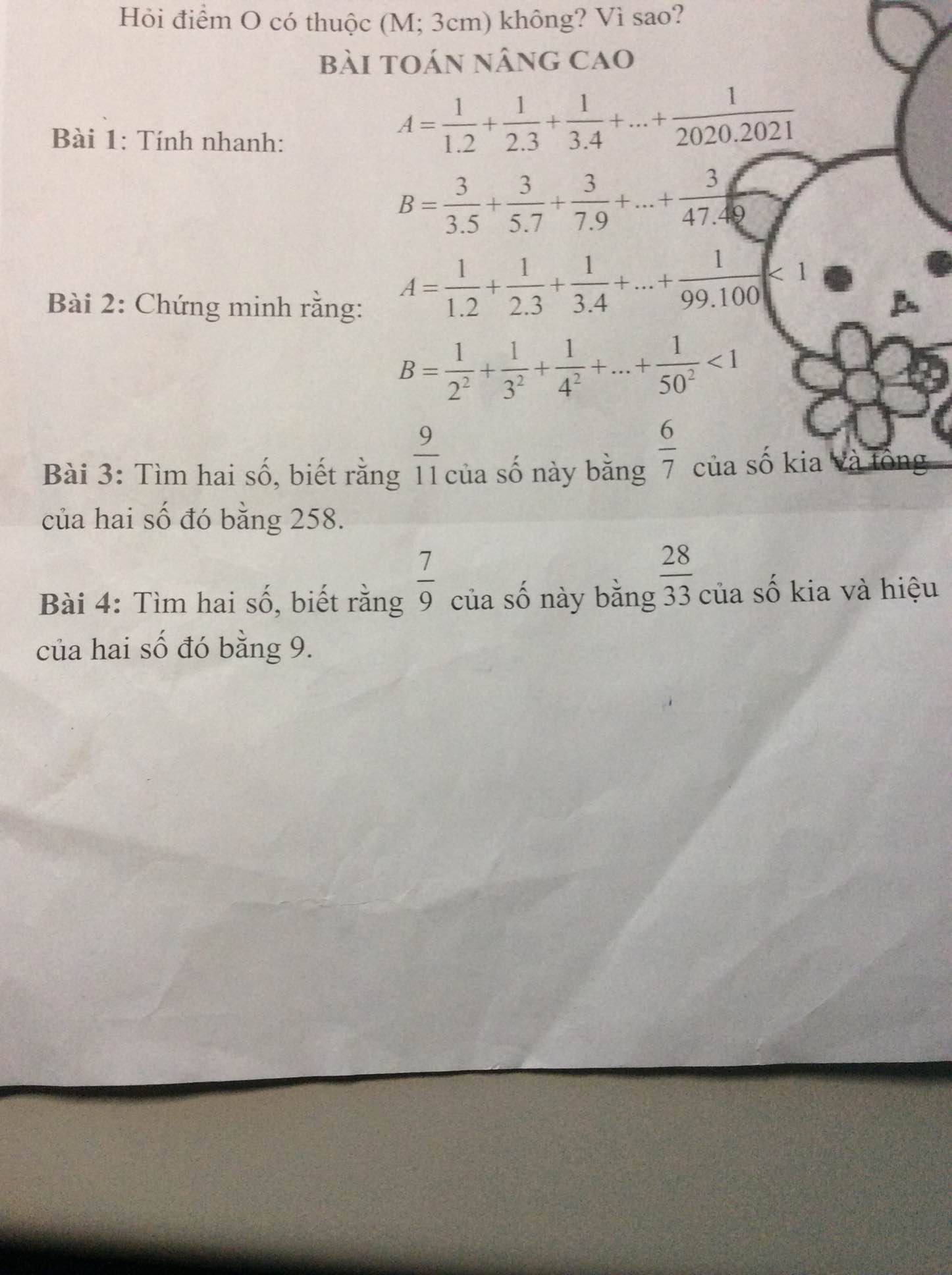


b: \(3^{300}=27^{100}\)
\(5^{200}=25^{100}\)
mà 27>25
nên \(3^{300}>5^{200}\)
cảm ơn bạn