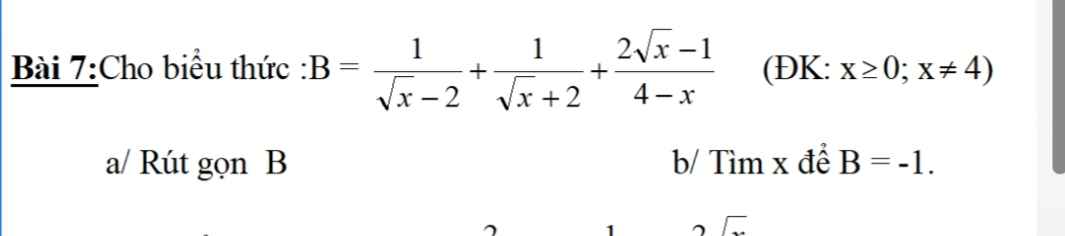
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1 is sleeping
2 tries
3 would give
4 be done
5 post - hasn't answered
6 were you doing - was
7 goes
8 is reading - doing
9 studies - will get
10 rang - was cooking

\(B=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+2+\sqrt{x}-2-2\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{x-4}\)
\(B=-1\Leftrightarrow\dfrac{1}{x-4}=-1\Rightarrow4-x=1\Rightarrow x=3\)



a)
f(x) + h(x) = g(x)
\( \Rightarrow x^4 - 3x^2 + x-1 \) + h(x) = \(x^4 - x^3 + x^2 +5\)
\(\Rightarrow \) h(x) = \(( x^4 - x^3 + x^2 + 5 ) - ( x^4 - 3x^2 + x-1 )\)
\(\Rightarrow \) h(x) = \(x^4 - x^3 + x^2 + 5 - x^4 + 3x^2 - x +1\)
\(\Rightarrow\) h(x) = \(( x^4-x^4 ) + ( -x^3 ) + ( x^2 + 3x^2 ) + ( 5+1)\)
\(\Rightarrow\) h(x) = \(4x^2 - x^3 +6\)
Vậy h(x) = \(4x^2 - x^3 +6\)
b) f(x) - h(x) = g(x)
\(\Rightarrow \) \(x^4 - 3x^2 +x-1\) - h(x) = \(x^4 - x^3 + x^2-1\)
\(\Rightarrow\) h(x) = \((x^4 - 3x^2 +x-1)\) - \((x^4 - x^3 + x^2 +5 )\)
\(\Rightarrow\) h(x) = \(x^4 - 3x^2 + x-1 - x^4 + x^3 - x^2 - 5\)
\(\Rightarrow\) h(x) = \(( x^4-x^4 ) + x^3 + ( -3x^2 - x^2 ) + ( -1-5 )\)
\(\Rightarrow\) h(x) = \(x^3 - 4x^2 -6\)
Vậy h(x) = \(x^3 - 4x^2 -6\)

vs đk tổng =1 ta có:
\(\dfrac{a+bc}{b+c}+\dfrac{b+ca}{c+a}+\dfrac{c+ab}{a+b}\)
\(=\dfrac{a\left(a+b+c\right)+bc}{bc}+\dfrac{b\left(a+b+c\right)+ca}{ca}+\dfrac{c\left(a+b+c\right)+ab}{ab}\)
\(=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\)
sd bđt AM-GM cho 2 số dương ta có:
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}\ge2\left(a+b\right)\)
\(\dfrac{\left(b+c\right)\left(b+a\right)}{c+a}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(b+c\right)\)
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(c+a\right)\left(c+b\right)}{a+b}\ge2\left(c+a\right)\)
Cộng theo vế 3 đẳng thức trên ta sẽ có điều phải chứng minh
Đẳng thức xảy ra khi và chỉ khi a = b= c =\(\dfrac{1}{3}\)

#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<p;
return 0;
}

 làm hộ mik với
làm hộ mik với