\(4x^2-24x+36=\left(x-3\right)^3\)
Tìm x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


PT ⇔ \(4x^2-24x+36=x^2-6x+9\)
⇔ \(3x^2-18x+27=0\)
⇔ \(\left(3x-9\right)\left(x-3\right)=0\)⇔ \(x=3\)

\(\frac{x^2+6x+9}{\left(x-1\right)^2}.\frac{2x^2-4x-2}{4x^2+24x+36}\)
\(=\frac{x^2+6x+9}{\left(x-1\right)^2}.\frac{2x^2-4x-2}{4\left(x^2+6x+9\right)}\)
\(=\frac{1}{\left(x-1\right)^2}.\frac{2x^2-4x-2}{4}\)
\(=\frac{2x^2-4x-2}{4x^2-8x+4}\)
\(\frac{x^2+6x+9}{\left(x-1\right)^2}.\frac{2x^2-4x-2}{4x^2+24x+36}\)
\(=\frac{x^2+2\left(x\right)\left(3\right)+3^2}{\left(x-1\right)^2}.\frac{2x^2-4x-2}{4x^2+24x+36}\)
\(=\frac{\left(x+3\right)^2}{\left(x-1\right)^2}.\frac{2x^2+4x-2}{4x^2+24x+36}\)
\(=\frac{\left(x+3\right)^2}{\left(x-1\right)^2}.\frac{2\left(x^2-2x-1\right)}{4x^2+24x+36}\)
\(=\frac{\left(x+3\right)^2}{\left(x-1\right)^2}.\frac{2\left(x^2-2x-1\right)}{4\left(x^2+2\left(x\right)\left(3\right)+3^2\right)}\)
\(=\frac{1}{\left(x-1\right)^2}.\frac{2\left(x^2-2x-1\right)}{4}\)
\(=\frac{1.2\left(x^2-2x-1\right)}{\left(x-1\right)^2.4}\)
\(=\frac{2\left(x^2-2x-1\right)}{4\left(x-1\right)^2}\)
\(=\frac{x^2-2x-1}{2\left(x-1\right)^2}\)

Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:

b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:

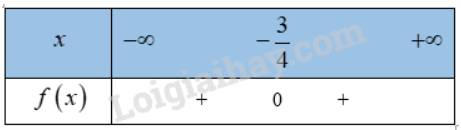
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:

1: Ta có: \(4x^2-36=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
2: Ta có: \(\left(x-1\right)^2+x\left(4-x\right)=11\)
\(\Leftrightarrow x^2-2x+1+4x-x^2=11\)
\(\Leftrightarrow2x=10\)
hay x=5

a) Ta có: \(\frac{x-4}{x+1}=\frac{x-15}{x+6}\)
\(\Rightarrow\)\(x^2+6x-4x-24=x^2-15x+x-15\)(nhân chéo)
\(\Rightarrow x^2+2x-24=x^2-14x-15\)
\(\Rightarrow16x=9\)
\(\Rightarrow x=\frac{9}{16}\)

a: \(A=\left(\dfrac{2\left(2x+1\right)}{2\left(2x+4\right)}-\dfrac{x}{3x-6}-\dfrac{2x^3}{3x^3-12x}\right):\dfrac{6x+13x^2}{24x-12x^2}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^3}{3x\left(x^2-4\right)}\right):\dfrac{x\left(13x+6\right)}{x\left(24-12x\right)}\)
\(=\left(\dfrac{2x+1}{2\left(x+2\right)}-\dfrac{x}{3\left(x-2\right)}-\dfrac{2x^2}{3\left(x-2\right)\left(x+2\right)}\right):\dfrac{13x+6}{-12\left(x-2\right)}\)
\(=\dfrac{3\left(2x+1\right)\left(x-2\right)-2x\left(x+2\right)-4x^2}{6\left(x+2\right)\left(x-2\right)}\cdot\dfrac{-12\left(x-2\right)}{13x+6}\)
\(=\dfrac{3\left(2x^2-3x-2\right)-2x^2-4x-4x^2}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{6x^2-9x-6-6x^2-4x}{x-2}\cdot\dfrac{-2}{13x+6}\)
\(=\dfrac{-\left(13x+6\right)\cdot\left(-2\right)}{\left(13x+6\right)\left(x-2\right)}=\dfrac{2}{x-2}\)
b: Để A>0 thì x-2>0
hay x>2
Để A>-1 thì A+1>0
\(\Leftrightarrow\dfrac{2+x-2}{x-2}>0\)
=>x/x-2>0
=>x>2 hoặc x<0

a) 6x2.(3x2 - 4x + 5) = 18x4 - 24x3 + 30x2
b) (x - 2y)(3xy + 6y2 + x) = 3x2y + 6xy2 + x2 - 6xy2 - 12y3 - 2xy = -12y3 + 3x2y - 2xy + x2
c) (18x4y3 - 24x3y4 + 12x3y3) : (-6x2y3) = -6x2y3(-3x2 + 4xy - 2x) : (-6x2y3) = 4xy - 3x2 - 2x
\(4x^2-24x+36=\left(x-3\right)^3\)
\(\Leftrightarrow4x^2-24x+36=x^3-9x^2+27x-27\)
\(\Leftrightarrow-x^3+13x^2-51x+63=0\)
\(\Leftrightarrow\left(-x^3+10x^2-21x\right)+\left(3x^2-30x+63\right)=0\)
\(\Leftrightarrow-x\left(x^2-10x+21\right)+3\left(x^2-10x+21\right)=0\)
\(\Leftrightarrow\left(x^2-10x+21\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left(x^2-3x-7x+21\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left[x\left(x-3\right)-7\left(x-3\right)\right]\left(3-x\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-7\right)\left(3-x\right)=0\)
\(\Leftrightarrow\left(3-x\right)^2\left(7-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(3-x\right)^2=0\\7-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=7\end{cases}}}\)
Vậy...
\(4x^2-24x+36=\left(x-3\right)^3\)\(\Leftrightarrow4\left(x^2-6x+9\right)=\left(x-3\right)^3\)
\(\Leftrightarrow4\left(x-3\right)^2=\left(x-3\right)^3\)\(\Leftrightarrow4\left(x-3\right)^2-\left(x-3\right)^3=0\)
\(\Leftrightarrow\left(x-3\right)^2\left[4-\left(x-3\right)\right]=0\)\(\Leftrightarrow\left(x-3\right)^2\left(4-x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\left(7-x\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}\left(x-3\right)^2=0\\7-x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x-3=0\\x=7\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=7\end{cases}}\)
Vậy \(x=3\)hoặc \(x=7\)