Tìm nghiệm nguyên (x,y) của phương trình x4-6x2+1=7.2y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x 4 - 6 x 2 + 3 = m
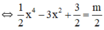
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng (d) y = m/2.
Từ đồ thị (C) nhận thấy :
+ m/2 < - 3 ⇔ m < -6
⇒ đường thẳng (d) không cắt đồ thị (C)
⇒ Phương trình vô nghiệm.
+ m/2 = -3 ⇔ m = -6
⇒ đường thẳng (d) cắt đồ thị (C) tại hai điểm cực tiểu
⇒ Phương trình có 2 nghiệm.
+ -3 < m/2 < 3/2 ⇔ -6 < m < 3
⇒ đường thẳng (d) cắt (C) tại 4 điểm phân biệt
⇒ Phương trình có 4 nghiệm.
+ m/2 = 3/2 ⇔ m = 3
⇒ đường thẳng (d) cắt (C) tại ba điểm
⇒ phương trình có 3 nghiệm.
+ m/2 > 3/2 ⇔ m > 3
⇒ đường thẳng (d) cắt (C) tại hai điểm
⇒ phương trình có hai nghiệm phân biệt.
Vậy:
+) m < - 6 thì phương trình vô nghiệm.
+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.
+) m = 3 thì PT có 3 nghiệm.
+) – 6 < m < 3 thì PT có 4 nghiệm.

Đáp án C
Đặt x 2 = t ( t ≥ 0 ) ta được phương trình t 2 - 6 t - 7 = 0 (*)
Nhận thấy a - b + c = 1 + 6 - 7 = 0 nên phương trình (*) có hai nghiệm
t 1 = -1(L); t 2 = 7(N)
Với t = 7 ta có x 2 = 7 ⇔ x = ± 7
Vậy phương trình đã cho có hai nghiệm.

Đặt x 2 = t (t ≥ 0) ta được phương trình t 2 – 6t – 7 = 0 (*)
Nhận thấy a – b + c = 1 + 6 – 7 = 0 nên phương trình (*) có hai nghiệm t 1 = − 1 ( L ) ; t 2 = 7 ( N )
Thay lại cách đặt ta có x 2 = 7 ⇔ x = ± 7
Vậy phương trình đã cho có hai nghiệm
Đáp án: C




Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...