Tính \(x^6-2x^4+x^3+x^2+x\) biết \(x^3-x=6\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A= x6 -x4 - x4 + x2 + (x3 -x) = x3(x3- x) - x(x3-x) + (x3-x) = (x3 - x)(x3- x +1)
A= 6(6+1) = 42

Bạn cần viết đề bài bằng công thức toán để được hỗ trợ tốt hơn.

Bài 2:
a: =a-b+c+a-c+b-b
=2a-b
b: =2x-5+x-a+x-5-a
=4x-10-2a


Ta có : \(x^2-2x-1=0
\)
\(\Leftrightarrow \)\((x-1)^2=2\)
\(\Leftrightarrow
\)\(\left[\begin{array}{}
x-1=\sqrt{2}\\
x-1=-\sqrt{2}
\end{array} \right.\)
Đặt P = \(\dfrac{x^6-6x^5+12x^4-8x^3+2015}{x^6-8x^3-12x^2+6x+2015}\)
=\(\dfrac{(x^6-2x^5-x^4)-(4x^5-8x^4-4x^3)+(5x^4-10x^3-5x^2)-(2x^3-4x^2-2x)+(x^2-2x-1)+2016}
{(x^6-2x^5-x^4)+(2x^5-4x^4-2x^3)+(5x^4-10x^3-5x^2)+(4x^3-8x^2-4x)+(x^2-2x-1)+12x+2016}\)
=\(\dfrac{x^4(x^2-2x-1)-4x^3(x^2-2x-1)+5x^2(x^2-2x-1)-2x(x^2-2x-1)+(x^2-2x-1)+2016}
{x^4(x^2-2x-1)+2x^3(x^2-2x-1)+5x^2(x^2-2x-1)+4x(x^2-2x-1)+(x^2-2x-1)+12x+2016}\)
=\(\dfrac{2016}{12x + 2016}\)
=\(\dfrac{2016}{12(x+1)+2004}\)
=\(\dfrac{168}{x+1+167}\)
=\(\left[\begin{array}{}
\dfrac{168}{\sqrt{2}+167}\\
\dfrac{168}{-\sqrt{2}+167}
\end{array} \right.\)
Chú thích: Hình như mẫu là \(-6x\) chứ không phải \(6x
\) bạn ạ. Hay là mình phân tích sai thì cho mình xin lỗi nhé.
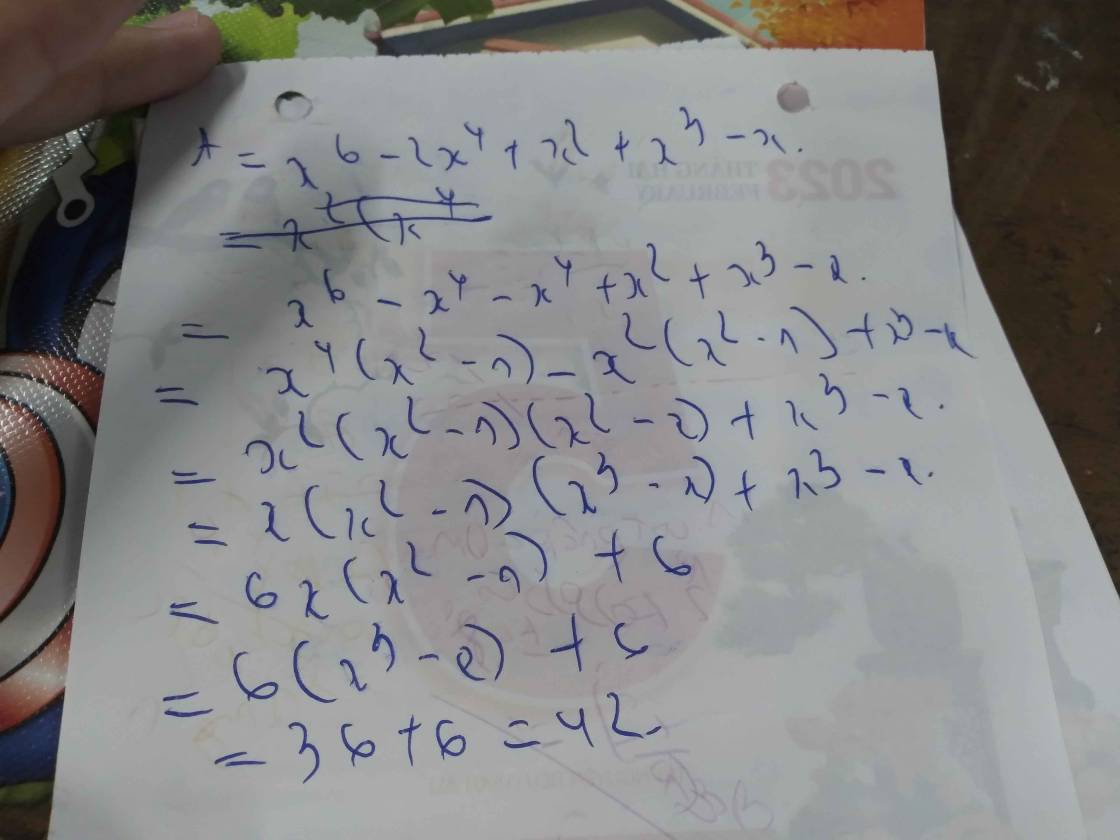
Chắc đề là thế này:v Còn không phải thì thôi nha !
\(x^6-2x^4+x^3+x^2-x\)
\(=\left(x^6-x^4\right)-\left(x^4-x^2\right)+\left(x^3-x\right)\)
\(=x^3\left(x^3-x\right)-x\left(x^3-x\right)+\left(x^3-x\right)\)
\(=6x^3-6x+x^3-x=7x^3-7x=7\cdot6=42\)