Tìm x biết
a)x2-2x=0
b)x2-7x+12=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3T
5
TM
15 tháng 11 2021
a/ \(x^2-25=0\)
\(\Rightarrow\left(x+5\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+5=0\Rightarrow x=-5\\x-5=0\Rightarrow x=5\end{matrix}\right.\)
b/ \(x\left(x+7\right)+x+7=0\)
\(x\left(x+7\right)+\left(x+7\right)=0\)
\(\left(x+7\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+7=0\Rightarrow x=-7\\x+1=0\Rightarrow x=-1\end{matrix}\right.\)
NQ
1
22 tháng 12 2021
a) \(\Rightarrow\left(x-1\right)\left(3x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-1\right)-2\left(x-1\right)=0\Rightarrow\left(x-1\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
7 tháng 9 2021
a: Ta có: \(\left(3x-2\right)\left(2x-1\right)-\left(6x^2-3x\right)=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
b: Ta có: \(x^3-\left(x+1\right)\left(x^2-x+1\right)=x\)
\(\Leftrightarrow x^3-x^3-1=x\)
hay x=-1
c: Ta có: \(56x^4+7x=0\)
\(\Leftrightarrow7x\left(8x^3+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
d: Ta có: \(x^2-5x-24=0\)
\(\Leftrightarrow\left(x-8\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-3\end{matrix}\right.\)
Bài 1.
10 tháng 12 2021
\(a,\Leftrightarrow2x^2+10x-2x^2=12\Leftrightarrow x=\dfrac{12}{10}=\dfrac{6}{5}\\ b,\Leftrightarrow\left(5-2x-4\right)\left(5-2x+4\right)=0\\ \Leftrightarrow\left(1-2x\right)\left(9-2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{9}{2}\end{matrix}\right.\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\\ d,\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ e,\Leftrightarrow4x^2-4x+1-4x^2+196=0\\ \Leftrightarrow-4x=-197\Leftrightarrow x=\dfrac{197}{4}\)
\(f,\Leftrightarrow x^2+8x+16-x^2+1=16\Leftrightarrow8x=-1\Leftrightarrow x=-\dfrac{1}{8}\\ g,Sửa:\left(3x+1\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(3x+1-x-1\right)\left(3x+1+x+1\right)=0\\ \Leftrightarrow2x\left(4x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\\ h,\Leftrightarrow x^2+8x-x-8=0\\ \Leftrightarrow\left(x+8\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-8\end{matrix}\right.\\ i,\Leftrightarrow2x^2-13x+15=0\\ \Leftrightarrow2x^2+2x-15x-15=0\\ \Leftrightarrow\left(x+1\right)\left(2x-15\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{15}{2}\end{matrix}\right.\)
18 tháng 8 2021
a) \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\Rightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\Rightarrow\left(2x-3\right)\left(7x-2x+3\right)=0\Rightarrow\left[{}\begin{matrix}2x-3=0\\5x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
b) \(\left(2x-7\right).\left(x-2\right)\left(x^2-4\right)=0\Rightarrow\left(2x-7\right)\left(x-2\right)^2\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}2x-7=0\\\left(x-2\right)^2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)
c)\(\left(9x^2-25\right)-\left(6x-10\right)=0\Rightarrow\left(3x-5\right)\left(3x+5\right)-2\left(3x-5\right)=0\Rightarrow\left(3x-5\right)\left(3x+5-2\right)=0\Rightarrow\left[{}\begin{matrix}3x-5=0\\3x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=1\end{matrix}\right.\)
18 tháng 8 2021
a: Ta có: \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\)
\(\Leftrightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{5}\end{matrix}\right.\)
b: Ta có: \(\left(2x-7\right)\left(x-2\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)^2\cdot\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)
c: Ta có: \(\left(9x^2-25\right)-\left(6x-10\right)=0\)
\(\Leftrightarrow\left(3x-5\right)\left(3x+5-2\right)=0\)
\(\Leftrightarrow\left(3x-5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)
21 tháng 7 2021
Bài 10:
a) (x+2)2 -x(x+3) + 5x = -20
=> x2 + 4x + 4 - x2 - 3x + 5x = -20
=> 6x = -20 + (-4)
=> 6x = -24
=> x = -4
b) 5x3-10x2+5x=0
=>5x(x2-2x+1)=0
=>5x(x-1)2 =0
=> 5x=0 hoặc (x-1)2=0
=>x=0 hoặc x=1
c) (x2 - 1)3 - (x4 + x2 + 1)(x2 - 1) = 0
=> (x2 - 1)[(x2 - 1)2 - (x4 + x2 + 1)] = 0
<=> (x2 - 1)(x4 - 2x2 + 1 - x4 - x2 - 1) = 0
<=> (x2 - 1)(-3x2) = 0
<=> (x2 - 1)=0 hoặc (-3x2) =0
<=> x2=1 hoặc x2=0
<=> x=−1;1 hoặc x=0
d)
(x+1)3−(x−1)3−6(x−1)2=-19
⇔x3+3x2+3x+1−(x3−3x2+3x−1)−6(x2−2x+1)+19=0
⇔x3+3x2+3x+1−x3+3x2−3x+1−6x2+12x−6+19=0
⇔12x+13=0⇔12x+13=0
⇔12x=-13
⇔x=-23/12
Học tốt nhé:333
23 tháng 11 2021
\(1,\\ a,ĐK:m\ne1\\ \Delta=49+48\left(m-1\right)=48m+1\\ \text{PT vô nghiệm }\Leftrightarrow48m+1< 0\Leftrightarrow m< -\dfrac{1}{48}\\ \text{PT có nghiệm kép }\Leftrightarrow48m+1=0\Leftrightarrow m=-\dfrac{1}{48}\\ \text{PT có 2 nghiệm phân biệt }\Leftrightarrow48m+1>0\Leftrightarrow m>-\dfrac{1}{48};m\ne1\)
\(b,\Delta=4\left(m-1\right)^2+4\left(2m+1\right)=4m^2+8>0,\forall m\\ \text{Vậy PT có 2 nghiệm phân biệt với mọi m}\\ 2,\\ \text{PT có 2 nghiệm phân biệt }\)
\(\Leftrightarrow\Delta=4\left(m+1\right)^2-4\left(m^2-1\right)>0\\ \Leftrightarrow4m^2+8m+4-4m^2+4>0\\ \Leftrightarrow8m+8>0\\ \Leftrightarrow m>-1\)
2 tháng 11 2021
Bài 1:
a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)
\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)
b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)
e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
CM
20 tháng 11 2017
a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
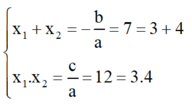
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
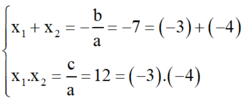
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.
a) \(x^2-2x=0\)
\(x\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}}\)
b) \(x^2-7x+12=0\)
\(x^2-4x-3x+12=0\)
\(\left(x^2-3x\right)-\left(4x-12\right)=0\)
\(x\left(x-3\right)-4\left(x-3\right)=0\)
\(\left(x-4\right)\left(x-3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-4=0\\x-3=0\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\x=3\end{cases}}}\)
a) \(x^2-2x=0\)
\(x\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}}\) \(\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
b) \(x^2-7x+12=0\)
\(x^2-3x-4x+12=0\)
\(\left(x^2-3x\right)-\left(4x-12\right)=0\)
\(x\left(x-3\right)-4\left(x-3\right)=0\)
\(\left(x-3\right)\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-4=0\end{cases}}\) \(\Rightarrow\orbr{\begin{cases}x=3\\x=4\end{cases}}\)