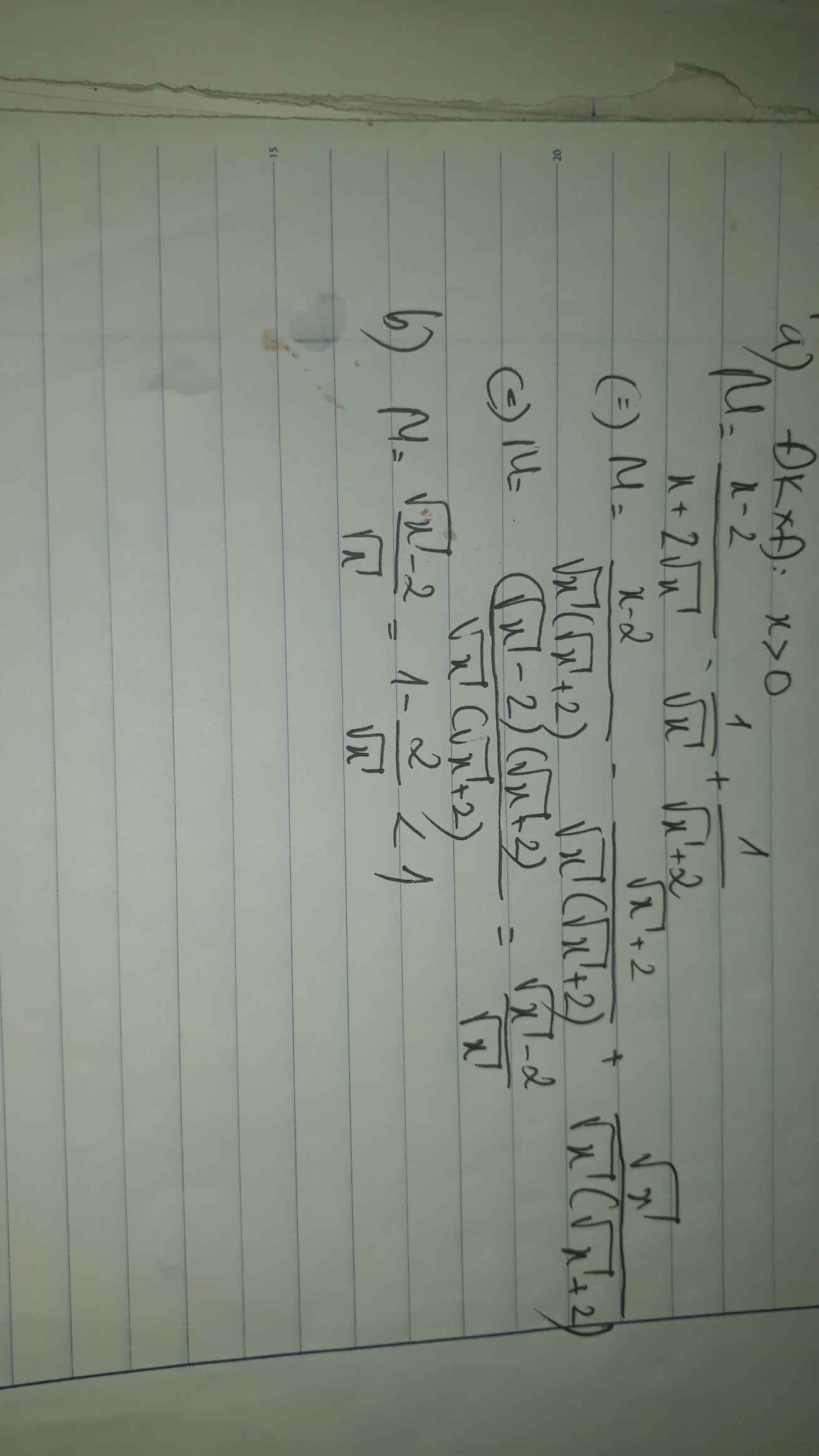so sánh √x + √(x+2) với 2√(x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 7 2019
a) Có \(x+1< x+2\)
\(\Rightarrow\sqrt{x+1}< \sqrt{x+2}\)
\(\Leftrightarrow\frac{\sqrt{x+1}}{\sqrt{x+2}}< 1\)
b) Vì \(\sqrt{x+1}< \sqrt{x+2}\)
\(\Rightarrow\sqrt{x+1}.\sqrt{x+1}.\sqrt{x+2}< \sqrt{x+2}.\sqrt{x+1}.\sqrt{x+1}\)
\(\Leftrightarrow\sqrt{x+1}^2.\sqrt{x+2}< \sqrt{x+2}^2.\sqrt{x+1}\)
\(\Rightarrow\frac{\sqrt{x+1}^2}{\sqrt{x+2}^2}< \frac{\sqrt{x+1}}{\sqrt{x+2}}\)
hay \(\frac{\sqrt{x+1}}{\sqrt{x+2}}>\frac{\sqrt{x+1}^2}{\sqrt{x+2}^2}\)
V
3
8 tháng 7 2018
\(\frac{x^2+x}{x^2+x+1}=\frac{x^3}{x^3+1}< 1\)1
* Giải thích: (Cái này bn chỉ cần giải thích bằng lời với ai đó hoặc ghi ra vở nháp thôi ko cần chép vào)
Vì tử (x3) bé hơn mẫu (x3+1) nên cả phân số đó bé hơn 1
Nếu bn thấy hợp lí thì k mk nhé!
Mơn bn! Iu
8 tháng 7 2018
cái chỗ mà \(1\)1 là chỉ có 1 số 1 thôi nhé. Mk lỡ tay ấn nhầm
20 tháng 7 2021
a) Ta có: \(M=\dfrac{x-2}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-2-\sqrt{x}-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
b) Ta có: M-1
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}}-\dfrac{\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{-2}{\sqrt{x}}< 0\forall x\) thỏa mãn ĐKXĐ
hay M<1
T
5 tháng 11 2023
\(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\left(dkxd:x\ge0;x\ne1\right)\)
\(=\left[\dfrac{x+2}{\left(\sqrt{x}\right)^3-1}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\left[\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right]\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{\left(x-2\sqrt{x}+1\right)\cdot2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\cdot\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2\cdot2}{\left(\sqrt{x}-1\right)^2\cdot\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
Xét: \(A-2=\dfrac{2}{x+\sqrt{x}+1}-2\)
\(=\dfrac{2}{x+\sqrt{x}+1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)
\(=\dfrac{2-2x-2\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{-2x-2\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\)
Với \(x\ge0;x\ne1\Leftrightarrow\left\{{}\begin{matrix}x+\sqrt{x}\ge0\\x+\sqrt{x}+1>0\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}\ge0\)
\(\Leftrightarrow\dfrac{-2\left(x+\sqrt{x}\right)}{x+\sqrt{x}+1}\le0\)
\(\Rightarrow A-2\le0\Leftrightarrow A\le2\)
Vậy: \(A\le2\).
MP
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1 2024
\(P=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\) với \(x\ge0\)
Ta có: \(P-1=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}-1=\dfrac{\sqrt{x}-2-2\sqrt{x}-1}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}+3}{2\sqrt{x}+1}\)
Do \(\sqrt{x}\ge0;\forall x\ge0\)
\(\Rightarrow\dfrac{\sqrt{x}+3}{2\sqrt{x}+1}>0\Rightarrow-\dfrac{\sqrt{x}+3}{2\sqrt{x}+1}< 0\)
\(\Rightarrow P-1< 0\Rightarrow P< 1\)
LL
1
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.
13 tháng 7 2019
a) Có vẻ đề o đúng lắm . Theo mình o phải là 11/11 mà 1/11
Ta có \(\frac{1}{11}>\frac{1}{12}>\frac{1}{13}>...>\frac{1}{19}>\frac{1}{20}\)
\(\Rightarrow\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+...+\frac{1}{19}+\frac{1}{20}>\frac{1}{20}+\frac{1}{20}+\frac{1}{20}+...+\frac{1}{20}=\frac{10}{20}=\frac{1}{2}\)
hay \(S>\frac{1}{2}\)
b)Ta có 1998 x 1999 + 3997=(2000-2) x 1999 +3997 = 2000 x 1999 - 2 x 1999 +3997 = 1999 x 2000 -3998 +3997 =1999 x 2000 -1
< 1999 x 2000 +2
=> 1999 x 2000 +2 / 1998 x 1999 +3997 > 1 hay M>1
BT
9 tháng 5 2017
2A=2/1.2.3 + 2/2.3.4 + 2/3.4.5 + ...+2/2014.2015.2016
Ta có: 2/1.2.3=1/1.2-1/2.3; 2/2.3.4=1/2.3-1/3.4; 2/3.4.5=1/3.4-1/4.5; ....; 2/2014.2015.2016=1/2014.2015-1/2015.2016
=> 2A=1/1.2-1/2015.2016
=> 2A < 1/2 => A < 1/4