5x-62=815:812
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2021
Đáp án:
P=±36P=±36
Giải thích các bước giải:
Ta có:
x2+y2+z2=16xy−yz+zx=−10⇒(x2+y2+z2)−2.(xy−yz+zx)=16−2.(−10)⇔x2+y2+z2−2xy+2yz−2zx=36⇔(x2−2xy+y2)+z2+2yz−2zx=36⇔(x−y)2+2z(y−x)+z2=36⇔(x−y)2−2.(x−y).z+z2=36⇔(x−y−z)2=36⇔x−y−z=±6P=x3−y3−z3−3xyz=(x3−3x2y+3xy2−y3)−z3+3x2y−3xy2−3xyz=(x−y)3−z3+3x2y−3xy2−3xyz=[(x−y)−z].[(x−y)2+(x−y).z+z2]+3xy(x−y−z)=(x−y−z).(x2−2xy+y2+xz−yz+z2+3xy)=(x−y−z).(x2+y2+z2+xy−yz+zx)Trường hợp 1: x−y−z=6⇒P=6.(16+(−10))=36Trường hợp 2: x−y−z=−6⇒P=(−6).(16+(−10))=−36x2+y2+z2=16xy−yz+zx=−10⇒(x2+y2+z2)−2.(xy−yz+zx)=16−2.(−10)⇔x2+y2+z2−2xy+2yz−2zx=36⇔(x2−2xy+y2)+z2+2yz−2zx=36⇔(x−y)2+2z(y−x)+z2=36⇔(x−y)2−2.(x−y).z+z2=36⇔(x−y−z)2=36⇔x−y−z=±6P=x3−y3−z3−3xyz=(x3−3x2y+3xy2−y3)−z3+3x2y−3xy2−3xyz=(x−y)3−z3+3x2y−3xy2−3xyz=[(x−y)−z].[(x−y)2+(x−y).z+z2]+3xy(x−y−z)=(x−y−z).(x2−2xy+y2+xz−yz+z2+3xy)=(x−y−z).(x2+y2+z2+xy−yz+zx)Trường hợp 1: x−y−z=6⇒P=6.(16+(−10))=36Trường hợp 2: x−y−z=−6⇒P=(−6).(16+(−10))=−36
Vậy P=±36P=±36.
PT
1
CM
31 tháng 7 2019
a. 38 762 + 49 363
+ 38762 49363 88125
b. 62 400 – 35 815
− 62400 35815 26585
CM
13 tháng 3 2019
Ta có: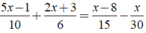
⇔ 15x - 3 + 10x + 15 = 2x - 16 - x
⇔ 25x - 2x + x = - 16 - 15 + 3
⇔ 24x = - 28 ⇔ x = - 7/6.
Vậy phương trình đã cho có tập nghiệm là S = { - 7/6 }.
Chọn đáp án C.
4T
2
NH
5 tháng 3 2023
1)
`x^2 -144=0`
`<=> x^2 =144`
\(< =>\left[{}\begin{matrix}x=12\\x=-12\end{matrix}\right.\)
2)`
`2x^2 -72=0`
`<=>2x^2 =72`
`<=>x^2=36`
\(< =>\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
3)
`5x^2 -125=0`
`<=> 5x^2 =125`
`<=>x^2 =25`
\(< =>\left[{}\begin{matrix}x=5\\x=-5\end{matrix}\right.\)
4)
`-x^2 +81=0`
`<=> x^2 -81=0`
`<=> x^2 =81`
\(< =>\left[{}\begin{matrix}x=9\\x=-9\end{matrix}\right.\)
5)
`x(2x-18)=0`
\(< =>\left[{}\begin{matrix}x=0\\2x-18=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)
KN
30 tháng 1 2019
a) \(-75+\left(-325\right)+\left|-45\right|-\left(-125\right)\)
\(=-75-325+45+125\)
\(=\left(45+125\right)-\left(75+325\right)\)
\(=170-400\)
\(=-230\)
b) \(62+\left|128\right|-\left|-155\right|-\left|70\right|\)
\(=62+128-155-70\)
\(\Leftrightarrow190-225\)
\(=-35\)
c) \(815+\left[95+\left(-815\right)+\left(-45\right)\right]\)
\(=815+95-815-45\)
\(=\left(815-815\right)+\left(95-45\right)\)
\(=0+50\)
\(=50\)
KN
30 tháng 1 2019
d) \(5+\left(-7\right)+9+\left(-11\right)+...+25+\left(-27\right)\)
\(=\left(5-7\right)+\left(9-11\right)+...+\left(25-27\right)\)
\(=-2-2-...-2\)
\(=-2.11\)
\(=-22\)
e) \(34+35+36+37-24-25-26-27\)
\(=\left(34-24\right)+\left(35-25\right)+\left(36-26\right)+\left(37-27\right)\)
\(=10+10+10+10\)
\(=40\)
10 tháng 8 2017
Số nguyên tố: 53, 91, 3869, 5251
Hợp số : 470, 60, 812, 28, 62, 11111. ( vì chúng có 3 ước trở lên).
DG
6
5x-36=83
5x-36= 512
5x =512+36=548
x = 109.6