abcde : mnpqr = ... (du 49993)
tim abcde
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 7 2019
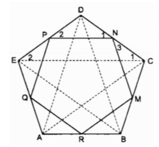
Xét △ ABC và △ BCD:
AB = BC (gt)
∠ B = ∠ C (gt)
BC = CD (gt)
Do đó: △ ABC = △ BCD (c.g.c)
⇒ AC = BD (1)
Xét △ BCD và △ CDE:
BC = CD (gt)
∠ C = ∠ D (gt)
CD = DE (gt)
Do đó: △ BCD = △ CDE (c.g.c) ⇒ BD = CE (2)
Xét △ CDE và △ DEA:
CD = DE (gt)
∠ D = ∠ E (gt)
DE = EA (gt)
Do đó: △ CDE = △ DEA (c.g.c) ⇒ CE = DA (3)
Xét △ DEA và △ EAB:
DE = EA (gt)
∠ E = ∠ A (gt)
EA = AB (gt)
Do đó: △ DEA = △ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong △ ABC ta có RM là đường trung bình
⇒ RM = 1/2 AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong Δ BCD ta có MN là đường trung bình
⇒ MN = 1/2 BD (tính chất đường trung bình của tam giác)
Trong △ CDE ta có NP là đường trung bình
⇒ NP = 1/2 CE (tính chất đường trung bình của tam giác)
Trong △ DEA ta có PQ là đường trung bình
⇒ PQ = 1/2 DA (tính chất đường trung bình của tam giác)
Trong △ EAB ta có QR là đường trung bình
⇒ QR = 1/2 EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: ∠ A = ∠ B = ∠ C = ∠ D = ∠ E = ((5-2 ). 180 0 )/5 = 108 0
△ DPN cân tại D
⇒ ∠ (DPN) = ∠ (DNP) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
△ CNM cân tại C
⇒ ∠ (CNM) = ∠ (CMN) = ( 180 0 - ∠ D )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (ADN) + ∠ (PNM) + ∠ (CNM) = 180 0
⇒ ∠ (PNM) = 180 0 - ( ∠ (ADN) + ∠ (CNM) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ BMR cân tại B
⇒ ∠ (BMR) = ∠ (BRM) = ( 180 0 - ∠ B )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (CMN) + ∠ (BRM) + ∠ (BMR) = 180 0
⇒ ∠ (NMR) = 180 0 - ( ∠ (CMN) + ∠ (BMR) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ ARQ cân tại A
⇒ ∠ (ARQ) = ∠ (AQR) = ( 180 0 - ∠ A )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (BRM) + ∠ (MRQ) + ∠ (ARQ) = 180 0
⇒ ∠ (MRQ) = 180 0 - ( ∠ (BRM) + ∠ (ARQ) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
△ QEP cân tại E
⇒ ∠ (EQP) = ∠ (EPQ) = ( 180 0 - ∠ E )/2 = ( 180 0 - 108 0 )/2 = 36 0
∠ (AQR) + ∠ (RQP) + ∠ (EQP) = 180 0
⇒ ∠ (RQP) = 180 0 - ( ∠ (AQR) + ∠ (EQP) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
∠ (EQP) + ∠ (QPN) + ∠ (DPN) = 180 0
⇒ ∠ (QPN) = 180 0 - ( ∠ (EPQ) + ∠ (DPN) )
= 180 0 - ( 36 0 – 36 0 ) = 108 0
Suy ra : ∠ (PNM) = ∠ (NMR) = ∠ (MRQ) = ∠ (RQP) = ∠ (QPN)
Vậy MNPQR là ngũ giác đều.
NT
2
DK
3
NM
2
TN
11 tháng 11 2018
\(abcde\times9=edcba\)
\(\Rightarrow a=1\Rightarrow e=9.\)
\(\Rightarrow1bcd9\times9=9dcb1\)
\(\Leftrightarrow\left(10009+10bcd\right)\times9=90001+10dcb\)
\(\Leftrightarrow8+9bcd=dcb\)
\(\Rightarrow b=1\) hoặc \(b=0\)
(loại b = 1.)
\(\Rightarrow b=0\)
\(\Rightarrow d=8\)
\(\Rightarrow10c89\times98c01\)
\(98001\le10c89\times9=98c01\le98901\)
\(10889\le10c89\le10989\)
\(10889\times9=98001\)
\(10989\times9=98901\)
\(\Rightarrow abcde=10989.\)
NT
2
15 tháng 10 2016
Ta gọi số 5 chữ số là ABCDE (A khác 0)
ABCDE
x 9
EDCBA
A = 1 (vì nếu A>1 thì tích sẽ có 6 chữ số)
=> E = 9
1BCD9
x 9
9DCB1
B = 0 hoặc B = 1 (vì nếu B >1 thì phép nhân ở hàng nghìn 9 x B sẽ nhớ ít nhất 1 sang hàng chục nghìn => E không thể là 9 được)
*) Xét trường hợp B = 0
10CD9
x 9
9DC01
=> 9.D + 8 có tận cùng là 0 => D = 8 (vì 9x8 + 8 = 80, tận cùng là 0)
10C89
x 9
98C01
Số 98C01 phải chia hết cho 9 => 9 + 8 + C + 0 + 1 = 18 + C chia hết cho 9 => C = 9
10989
x 9
98901
Đúng. Vậy ta được 1 đáp số là 10989
*) Xét trường hợp B = 1 (sau khi đã biết A = 1, D = 9)
11CD9
x 9
9DC11
=> 9.D + 8 có tận cùng là 1
=> D = 7 (vì 9.7 + 8 = 71, có tận cùng là 1)
11C79
x 9
97C11
Số 97C11 phải chia hết cho 9 => 9 + 7 + C + 1 + 1 = 18 + C chia hết cho 9 => C = 0 hoặc C = 9
Thử lại với C = 0:
11079
x 9
97011 KHÔNG ĐÚNG
Thử lại với C = 9
11979
x 9
97911 KHÔNG ĐÚNG
Vậy có 1 đáp số duy nhất là:
10989
x 9
98901
VT
1
24 tháng 12 2015
\(\frac{a}{9}=\frac{bcde}{1234}=1\) ( vì b >/ 1)
=> a=9 ; bcde=1234
=> abcde=91234
NV
0