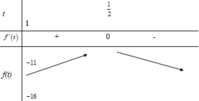
Tìm m để phương trình x4-3x3=m có 4 nghiệm phân biệt x\(\in\)\((\)-1;2\()\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(x^2=t\left(t\ge0\right)\), phương trình trở thành:
\(t^2-2\left(m+1\right)t+2m+1=0\left(1\right)\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2>0\\t_1+t_2=2m+2>0\\t_1t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m\ne0\end{matrix}\right.\)

| x 4 – 5 x 2 + 4 |
Đáp án D
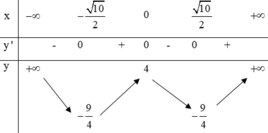
Xét hàm y = x 4 – 5 x 2 + 4
⇒ y’ = 4x3 – 10x
⇒ y’ = 0 ó x = 0 hoặc x = ± 5 2
Ta có bảng biến thiên
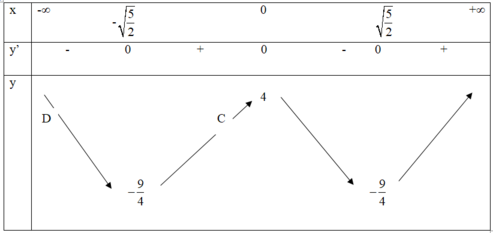
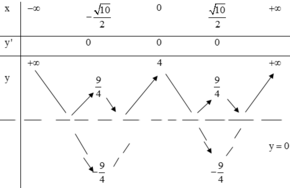
Ta có bảng biến thiên hàm y = | x 4 – 5 x 2 + 4 |
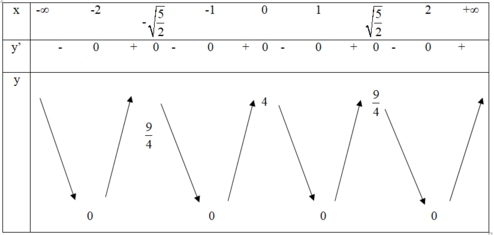
Vậy phương trình có 8 nghiệm ó đường y = m giao đồ thị hàm số y = | x 4 – 5 x 2 + 4 | tại 8 điểm phân biệt
⇔ 0 < m < 9 4

b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
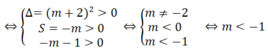


Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
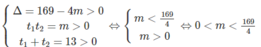

Đáp án D
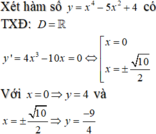


Bước 1: Ta giữ nguyên phần đồ thị phía trên trục hoành.
Bước 2: Lấy đối xứng phần phía dưới trục hoành của đồ thị lên phía trên trục hoành và xóa bỏ đi phần đồ thị nằm phía dưới trục hoành ta được đồ thị hàm số y = x 4 - 5 x 2 + 4
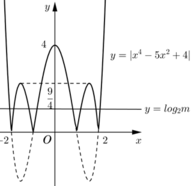
Khi đó số nghiệm của phương trình x 4 - 5 x 2 + 4 = log 2 m chính là số giao điểm của đồ thị hàm số y = x 4 - 5 x 2 + 4 và đường thẳng y = log 2 m với m > 0.Dựa vào đồ thị hàm số y = x 4 - 5 x 2 + 4 ta thấy để phương trình x 4 - 5 x 2 + 4 = log 2 m có 8 nghiệm thì: 0 < log 2 m < 9 4 ⇔ 1 < m < 2 9 4

Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2

\(x^4-1-mx^2+m=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)-m\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=m-1\end{matrix}\right.\)
Pt có 4 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ne2\end{matrix}\right.\)
Khi đó ta có:
\(\left|x_1-x_2\right|=\left|1-\sqrt{m-1}\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{m-1}=1\\1-\sqrt{m-1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=5\end{matrix}\right.\)
Vậy \(m_0=5\)