hàm số y=-x^2+2x+m-4 đạt GTLN trên [-1;2] bằng 3 khi m thuộc khoảng đoạn nào
AI GIẢI ĐƯỢC LỜI GIẢI RÕ RÀNG CHI TIẾT ĐẦY ĐỦ MÌNH TICK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thị Thùy Dung
5 tháng 2 2023
Đúng(1)
Những câu hỏi liên quan
KH
1
CM
27 tháng 4 2019
Chọn A
Tập xác định 
Ta có: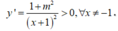 
Suy ra hàm số y =
x
-
m
2
x
+
1
đồng biến trên 
Do đó: 
Theo giả thiết: 
N
0
CM
19 tháng 2 2019
* Hàm số đã cho liên tục trên R vì với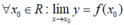 
nên (1) đúng
* Tại điểm x = 0 hàm số không có đạo hàm nên (2) sai.
* y = x 2 - 2 | x | + 2 = | x | 2 - 2 | x | + 2 = ( | x | - 1 ) 2 + 1 ≥ 1 ∀ x
Suy ra, GTNN của hàm số là 1 khi |x| = 1 ⇔ x = ±1
nên hàm số không có GTLN.
* Phương trình x 2 - 2 | x | + 2 = 0 vô nghiệm nên đồ thị không cắt trục hoành.
f ( - x ) = ( - x ) 2 - 2 | - x | + 2 = x 2 - 2 | x | + 2 = f ( x )
Nên hàm số đã cho là hàm số chẵn.
Mệnh đề 1, 5 đúng. Mệnh đề 2, 3,4,6 sai.
Chọn B
CM
26 tháng 4 2017
Xét
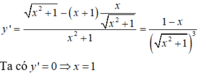
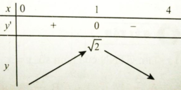
Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng √2 khi x = 1 . Chọn đáp án A.
RH
2 tháng 1 2022
y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2022
a.
\(y=x^2\left(4-2x\right)=x.x.\left(4-2x\right)\le\left(\dfrac{x+x+4-2x}{3}\right)^3=\dfrac{64}{27}\)
\(y_{max}=\dfrac{64}{27}\) khi \(x=4-2x\Rightarrow x=\dfrac{4}{3}\)
b.
\(y=x\left(2-x\right)^2=\dfrac{1}{2}.2x.\left(2-x\right)\left(2-x\right)\le\dfrac{1}{2}\left(\dfrac{2x+2-x+2-x}{3}\right)^3=\dfrac{32}{27}\)
\(y_{max}=\dfrac{32}{27}\) khi \(2x=2-x\Rightarrow x=\dfrac{2}{3}\)
L
1
19 tháng 3 2018
Ta có :
\(2x^2+\dfrac{1}{x^2}+\dfrac{y^2}{4}=4\)
\(\Rightarrow\left(x^2+\dfrac{1}{x^2}-2\right)+\left(x^2+\dfrac{y^2}{4}-xy\right)=2-xy\)
\(\Rightarrow\left(x-\dfrac{1}{x}\right)^2+\left(x-\dfrac{y}{2}\right)^2=2-xy\)
Ta có:
\(\left(x-\dfrac{1}{x}\right)^2\ge0\forall x\)
\(\left(x-\dfrac{y}{2}\right)^2\ge0\forall x,y\)
\(\Rightarrow\left(x-\dfrac{1}{x}\right)^2+\left(x-\dfrac{y}{2}\right)^2\ge0\forall x,y\)
\(\Rightarrow2-xy\ge0\forall x,y\)
\(\Rightarrow xy\le2\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x-\dfrac{1}{x}=0\\x-\dfrac{y}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{x}\\x=\dfrac{y}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x^2=1\\y=2x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\end{matrix}\right.\)
Vậy (x;y) nguyên thỏa mãn là : (1;2);(-1;-2)