Tìm đa thức dư khi chia x2019 + x2 + 1 cho x3 - x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rõ ràng đa thức \(x^3-1\) chia hết cho đa thức \(x^2+x+1\).
Ta tách: \(x^9+x^6+x^3+1=\left(x^9-1\right)+\left(x^6-1\right)+\left(x^3-1\right)+4=\left(x^3-1\right)\left(x^6+x^3+1\right)+\left(x^3-1\right)\left(x^3+1\right)+\left(x^3-1\right)+4\).
Từ đây suy ra đa thức đó chia cho đa thức \(x^2+x+1\) được đa thức dư là 4.

a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.

Ta có

Phần dư của phép chia trên là R = (a + 4)x + b
Theo bài ra ta có (a + 4)x + b = 2x – 3 ó a + 4 = 2 b = - 3 ó a = - 2 b = - 3
Vậy giá trị của a và b thỏa mãn điều kiện đề bài là a = -2; b = -3
Đáp án cần chọn là: D

2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)


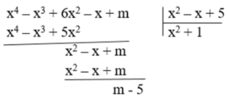
Giải
Ta thấy đa thức dư trong phép chia có dạng ax2 + bx + c
Đặt x2019 + x + 1 = ( x3 - x ) . g( x ) + a2 +bx +c
+) Với x = 0 ta được 1 = c
+) Với x =1 ta được 3 = a + b +1
=> a + b = 2 ( 1 )
+) Với x= -1 ta được 1 = a -b + 1
=> a -b = 0 ( 2 )
Từ ( 1 ) và ( 2 )
=> a=b=1
Vậy đa thức dư là x2 + x + 1