Tìm hai số nguyên tố sao cho tổng và hiệu đều là số nguyên tố
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 10 2019
Gọi a, b, c, d là các số nguyên tố. (a>b)
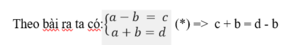
Từ (*) ⇒ a > 2, a là số nguyên tố lẻ ⇒ c + b và d – b là số lẻ. Do b, c, d đều là số nguyên tố nên để c + b và d – b là số lẻ thì ⇒ b chẵn. Vậy b = 2
a. Bài toán đưa về dạng tìm một số nguyên tố a sao cho a – 2 và a + 2 cũng là số nguyên tố.
- Nếu a = 5 ⇒ a – 2 = 3; a + 2 = 7 đều là số nguyên tố
- Nếu a ≠ 5 . Xét 2 trường hợp
+ a chia 3 dư 1 ⇒ a + 2 chia hết cho 3 : không là số nguyên tố
+ a chia 3 dư 2 ⇒ a – 2 chia hết cho 3: không là số nguyên tố
Vậy chỉ có số nguyên tố a duy nhất thoả mãn là 5.
Hai số nguyên tố cần tìm là 5; 2
PT
0
VV
1
13 tháng 10 2015
2 và 5
vì 5-2=3(số nguyên tố)
5+2=7(số nguyên tố)
Tick đúng cho mình nha
21 tháng 10 2015
1) +) Nếu cả hai số nguyên tố đều > 3 => 2 số đó lẻ => tổng và hiệu của chúng là số chẵn => Loại
=> Trong hai số đó có 1 số bằng 2. gọi số còn lại là a
+) Nếu a = 3 : ta có 3 + 2 = 5 ; 3 -2 = 1, 1 không là số nguyên tố => Loại
+) Nếu > 3 thì có thể có dạng: 3k + 1 ( k \(\in\)N*) hoặc 3k + 2 (k \(\in\) N*)
Khi a = 3k + 1 => a+ 2 = 3k + 3 = 3.(k + 1) là hợp số với k \(\in\) N* => Loại
Khi a = 3k + 2 => a + 2 = 3k + 4 ; a - 2 = 3k . 3k; 3k + 4 đều là số nguyên tố với k = 1 . Với k > 1 thì 3k là hợp số nên Loại
Vậy a = 3. 1+ 2 = 5
Vậy chỉ có 2 số 2;5 thỏa mãn
PH
30 tháng 10 2021
Bài 1: p = 4
Bài 2: p =3
Bài 3. p = 2
Bài 4: ....... tự giải đi
Lần sau hỏi bài của lớp 6 thì đừng hỏi ở đây
NT
0
Số 5 và 2 được ko?
Tổng và tích chứ nhỉ? E bị sai đề thì phải á