các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm của các cạnh BC,CA,AB của tam giác ABC. Tọa độ đỉnh A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
21 tháng 10 2017
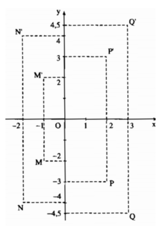
Gọi M’, N’, P’, Q’ là các điểm lần lượt đối xứng qua các điểm M, N, P, Q qua trục Ox, ta thấy rằng hoành độ của các điểm đối xứng nhau qua trục hoành bằng nhau, còn tung độ của các điểm đó thì đối nhau: M’(-1; 2); N’(-2; 4); P’(2; 3); Q’(3; 4,5).

25 tháng 8 2023
M' đối xứng M qua Ox
=>\(\left\{{}\begin{matrix}x_{M'}=-x_M=1\\y_{M'}=y_M=-2\end{matrix}\right.\)
N' đối xứng N qua Ox
=>\(\left\{{}\begin{matrix}x_{N'}=-x_N=2\\y_{N'}=y_N=-4\end{matrix}\right.\)
P' đối xứng P qua Ox
=>\(\left\{{}\begin{matrix}x_{P'}=-x_P=-2\\y_{P'}=y_P=-3\end{matrix}\right.\)
Q' đối xứng Q qua Ox
=>\(\left\{{}\begin{matrix}x_{Q'}=-x_Q=-3\\y_{Q'}=y_Q=-4,5\end{matrix}\right.\)
Có \(\left\{{}\begin{matrix}x_M=\frac{x_B+x_C}{2}\\y_M=\frac{y_B+y_C}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4=x_B+x_C\\6=y_B+y_C\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_N=\frac{x_C+x_A}{2}\\y_N=\frac{y_C+y_A}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C+x_A=0\\y_C+y_A=-8\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_P=\frac{x_A+x_B}{2}\\y_P=\frac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2=x_A+x_B\\12=y_A+y_B\end{matrix}\right.\)
Bạn tự giải hpt để tìm, cái này tìm đc luôn 3 đỉnh chứ ko phải mỗi đỉnh A
Gọi I là trung điểm NP \(\Rightarrow I\left(-\frac{1}{2};1\right)\)
Do NP là đường trung bình của tam giác và M là trung điểm BC
\(\Rightarrow\) I là trung điểm AM
\(\Rightarrow\left\{{}\begin{matrix}x_A=2x_I-x_M=-3\\y_A=2y_I-y_M=-1\end{matrix}\right.\) \(\Rightarrow A\left(-3;-1\right)\)