cho a+b= -6 và a^2+b^2=80. Tính M=a^3+b^3(áp dụng tách 1 hạng tử thành 2 hạng tử)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HB
2
12 tháng 7 2017
a)
\(x^3-7x-6=x^3+1-7x-7\)
= \(\left(x+1\right)\left(x^2-x+1\right)-7\left(x+1\right)\)
= \(\left(x+1\right)\left(x^2-x+1-7\right)\)
= \(\left(x+1\right)\left(x^2-x-6\right)\)
b)
\(x^3-5x^2-14x=x^3+2x^2-7x^2-14x\)
= \(x^2\left(x+2\right)-7x\left(x+2\right)\)
= \(\left(x^2-7x\right)\left(x+2\right)\)
= \(x\left(x-7\right)\left(x+2\right)\)
12 tháng 7 2017
a,x^3 -x-6x-6 = x(x^2 -1)-6(x+1)= x(x-1)(x+1)-6(x+1)=(x+1)(X^2-x-6)=(x+1)(x^2+2x-3x-6)=(x+1)(x(x+2)-3(x+2))=(x+1)(x+2)(x-3)
b,x(x^2-5x-14)=x(x^2+2x-7x-14)=x(x(x+2)-7(x+2))=x(x+2)(x-7)
NT
30 tháng 10 2017
a) \(=x^2-2x-4x+8\)
\(=x\left(x-2\right)-4\left(x-2\right)\)
\(=\left(x-2\right)\left(x-4\right)\)
c) \(=x^3-x-6x-6\)
\(=x\left(x^2-1\right)-6\left(x+1\right)\)
\(=x\left(x+1\right)\left(x-1\right)-6\left(x+1\right)\)
\(=x\left(x+1\right)\left(x-1-6\right)\)
\(=x\left(x+1\right)\left(x-7\right)\)
FN
1
VT
10 tháng 1 2018
cái này chính là BĐT \(a^2+b^2+c^2\ge ab+bc+ca\Leftrightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ca\right)\)
<=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
với c=1 tì ta luôn có ĐPCM
JK
24 tháng 7 2019
a, 3x^2 + 13x + 10
= 3x^2 + 3x + 10x + 10
= 3x(x + 1) + 10(x + 1)
= (3x + 10)(x + 1)
b, x^2 - 10x + 21
= x^2 - 3x - 7x + 21
= x(x - 3) - 7(x - 3)
= (x - 7)(x - 3)
c, 6x^2 - 5x + 1
= 6x^2 - 3x - 2x + 1
= 3x(2x - 1) - (2x - 1)
= (3x - 1)(2x - 1)
24 tháng 7 2019
Bạn đăng 1 lần nhiều bài như vậy làm người khác nản lắm đấy =) đơn giản bài rất dài mà mik cx ko chắc là bản thân mik có đc k hay ko nên phải nản vậy thôi :)
1a)\(3x^2+13x+10=3x^2+3x+10x+10\)
\(3x\left(x+1\right)+10\left(x+1\right)=\left(3x+10\right)\left(x+1\right)\)
b)\(x^2-10x+21=x^2-3x-7x+21\)
\(=x\left(x-3\right)-7\left(x-3\right)=\left(x-7\right)\left(x-3\right)\)
c)\(6x^2-5x+1=6x^2-3x-2x+1\)
\(=3x\left(2x-1\right)-\left(2x-1\right)=\left(3x-1\right)\left(2x-1\right)\)
H9
HT.Phong (9A5)
CTVHS
22 tháng 10 2023
a) \(x^3+4x^2-21x\)
\(=x\left(x^2+4x-21\right)\)
\(=x\left(x^2-3x+7x-21\right)\)
\(=x\left[x\left(x-3\right)+7\left(x-3\right)\right]\)
\(=x\left(x-3\right)\left(x+7\right)\)
b) \(5x^3+6x^2+x\)
\(=x\left(5x^2+6x+1\right)\)
\(=x\left(5x^2+5x+x+1\right)\)
\(=x\left[5x\left(x+1\right)+\left(x+1\right)\right]\)
\(=x\left(x+1\right)\left(5x+1\right)\)
c) \(x^3-7x+6\)
\(=x^3+2x^2-3x-2x^2-4x+6\)
\(=x\left(x^2+2x-3\right)-2\left(x^2+2x-3\right)\)
\(=\left(x-2\right)\left(x^2+2x-3\right)\)
\(=\left(x-2\right)\left(x-1\right)\left(x+3\right)\)
d) \(3x^3+2x-5\)
\(=3x^3+3x^2+5x-3x^2-3x-5\)
\(=x\left(3x^2+3x+5\right)-\left(3x^2+3x+5\right)\)
\(=\left(x-1\right)\left(3x^2+3x+5\right)\)
14 tháng 8 2021
a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)
3 tháng 9 2016
1) \(^{x^2\left(a+b-c\right)+x\left(a+b-c\right)}\)
\(=\left(x^2+x\right)\left(a+b-c\right)\)
\(=x\left(x+1\right)\left(a+b-c\right)\)
2) \(m\left(a^2-b^2\right)+n\left(a^2-b^2\right)=\left(m+n\right)\left(a^2-b^2\right)\)
3) \(12x^2-13x+3=12x^2-9x-4x+3\)
\(=3x\left(4x+3\right)-\left(4x+3\right)=\left(3x-1\right)\left(4x+3\right)\)
4) \(15x^2-31x+2=15x^2-30x-x+2\)
\(=15x\left(x-2\right)-\left(x-2\right)\)\(=\left(15x-1\right)\left(x-2\right)\)
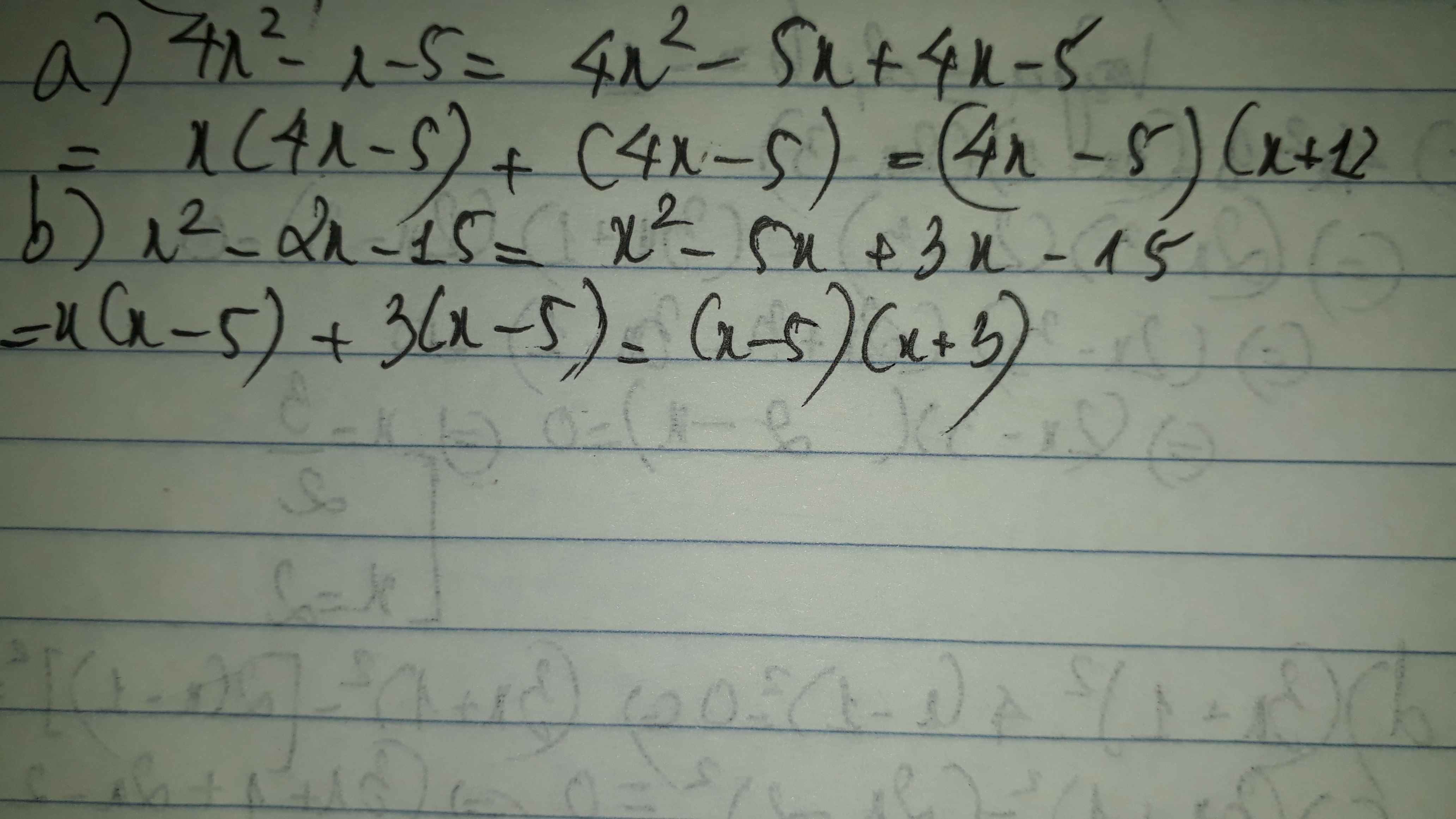
Ta có: a2 + b2 = 80
=> (a2 + 2ab + b2) - 2ab = 80
=> (a + b)2 - 2ab = 80
=> (-6)2 - 2ab = 80
=> 2ab = 36 - 80
=> 2ab = -44
=> ab = -22
Khi đó: M = a3 + b3 = (a + b)(a2 - ab + b2) = -6.[80 - (-22)] = -6.102 = -612