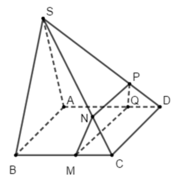
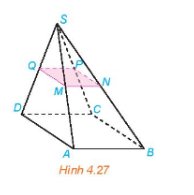
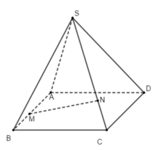
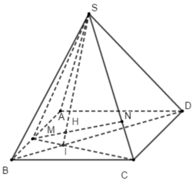
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy các điểm M, N, P, Q lần lượt thuộc các cạnh BC, SC, AD sao cho MN//SB; NP//CD; MQ//CD.
a) Chứng minh: PQ//(SAB).
b) Gọi K là giao điểm của MN và PQ. Chứng minh rằng K luôn chạy trên một đường thẳng cố định.

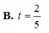
Ta có AB//CD \(\Rightarrow\) AB//(MNPQ)
SB//MN \(\Rightarrow\) SB//(MNPQ)
\(\Rightarrow\) (SAB)//(MNPQ)
Mà \(\left\{{}\begin{matrix}SA=\left(SAD\right)\cap\left(SAB\right)\\PQ=\left(SAD\right)\cap\left(MNPQ\right)\end{matrix}\right.\) \(\Rightarrow\) SA//PQ
b/ Ta có \(K\in\left(SAD\right);K\in\left(SBC\right)\Rightarrow SK=\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow K\) thuộc giao tuyến (SAD) và (SBC)
Mà giao tuyến (SAD) và (SBC) là đường thẳng cố định qua S song song AD và BC \(\Rightarrow\) K thuộc 1 đường thẳng cố định