cho tam giác ABCvuông tại A,biếtAB=9,C=3độ
a giải tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


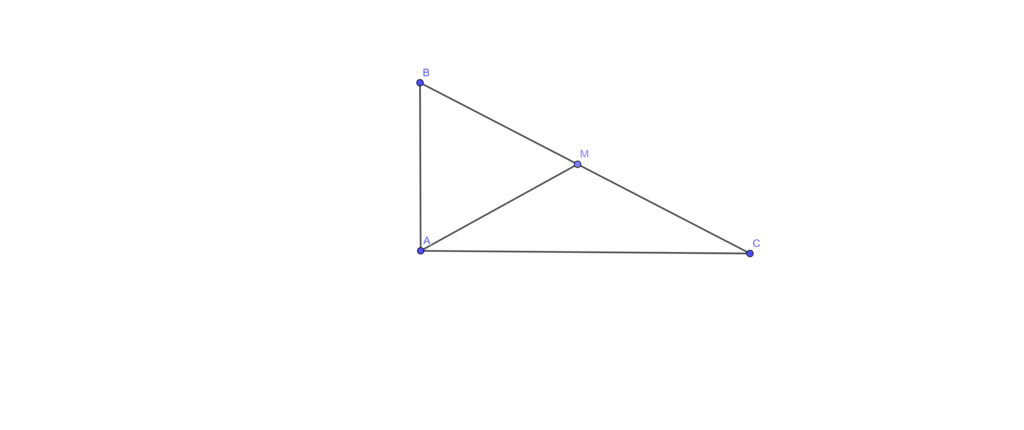
Xét ΔABM có : BA=BM
=> ΔABM cân tại B
=> \(\widehat{BAM}=\widehat{B}=30^o\)
=> \(\widehat{MAC}=90^o-30^o=60^o\)
\(\widehat{C}=90^o-\widehat{B}=60^o\)
ΔAMC có 2 góc \(60^o\)
=> ΔAMC là tam giác đều

b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB

a: Xét ΔBAM vuông tại A và ΔBNM vuông tại N có
BM chung
góc ABM=góc nBM
=>ΔBAM=ΔBNM
b: ΔBAM=ΔBNM
=>BA=BN