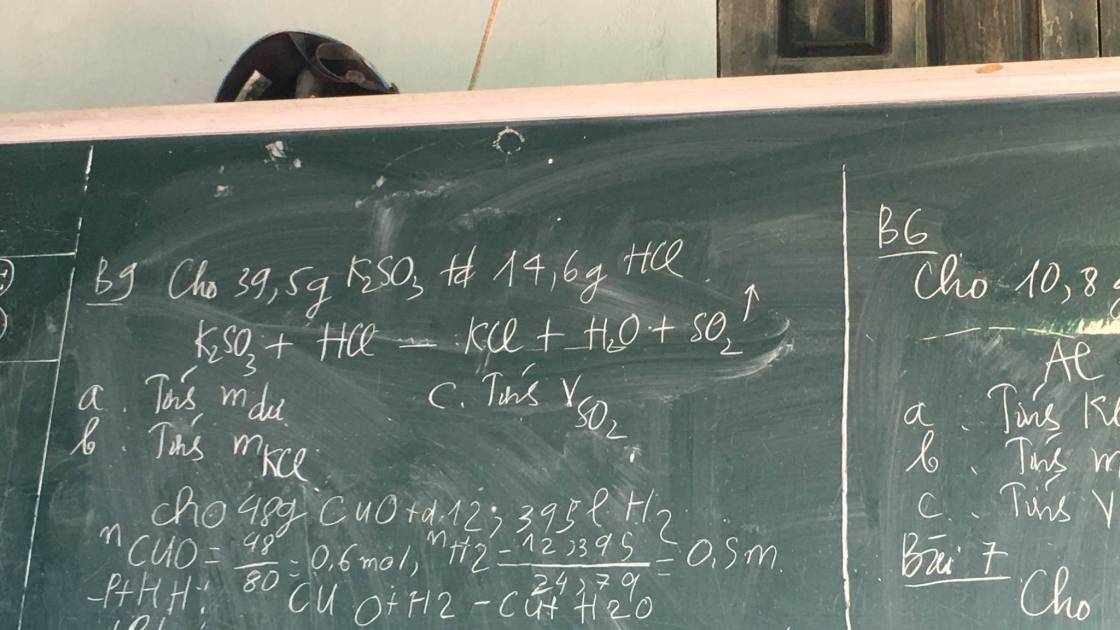Giải hộ em bài 8, 9 với ạ. Em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MA
1
23 tháng 11 2021
a) \(P=U.I\Rightarrow I=\dfrac{P}{U}=\dfrac{75}{220}=\dfrac{15}{44}\left(A\right)\)
b) \(A=P.t=75.30.4.60.60=32400000\left(J\right)=9\left(kWh\right)\)
c) Tiền điện phải trả: \(9.2000=18000\left(đồng\right)\)
MB
3
20 tháng 10 2021
Câu 12.
\(5\sqrt{a}+6\sqrt{\dfrac{a}{4}}-a\sqrt{\dfrac{4}{a}}+5\sqrt{\dfrac{4a}{25}}\)
\(=5\sqrt{a}+6\dfrac{\sqrt{a}}{2}-a\cdot\dfrac{2}{\sqrt{a}}+5\dfrac{2\sqrt{a}}{5}\)
\(=5\sqrt{a}+3\sqrt{a}-2\sqrt{a}+2\sqrt{a}\) (vì a>0)
\(=8\sqrt{a}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)
QH
0
F
17 tháng 4 2022
\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)
Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)
\(\left(sinx+cosx\right)'=cosx-sinx\)
Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)
19 tháng 7 2023
\(n_{K_2SO_3}=\dfrac{39,5}{158}=0,25\left(mol\right)\) ; \(n_{HCl}=\dfrac{14,6}{36,5}=0,4\left(mol\right)\)
\(K_2SO_3+HCl\rightarrow KCl+H_2O+SO_2\)
\(0,25\) \(0,4\)
→ HCl dư
\(K_2SO_3+HCl\rightarrow KCl+H_2O+SO_2\)
\(0,25\rightarrow0,25\rightarrow0,25\rightarrow0,25\rightarrow0,25\)
a) m dư = m K2SO3 = 0,25 . 158 = 39,5 (g)
b) m KCl = 0,25 . 74,5 = 18,625 (g)
c) V SO2 = 0,25 . 22,4 = 5,6 (lít)
5 tháng 11 2021
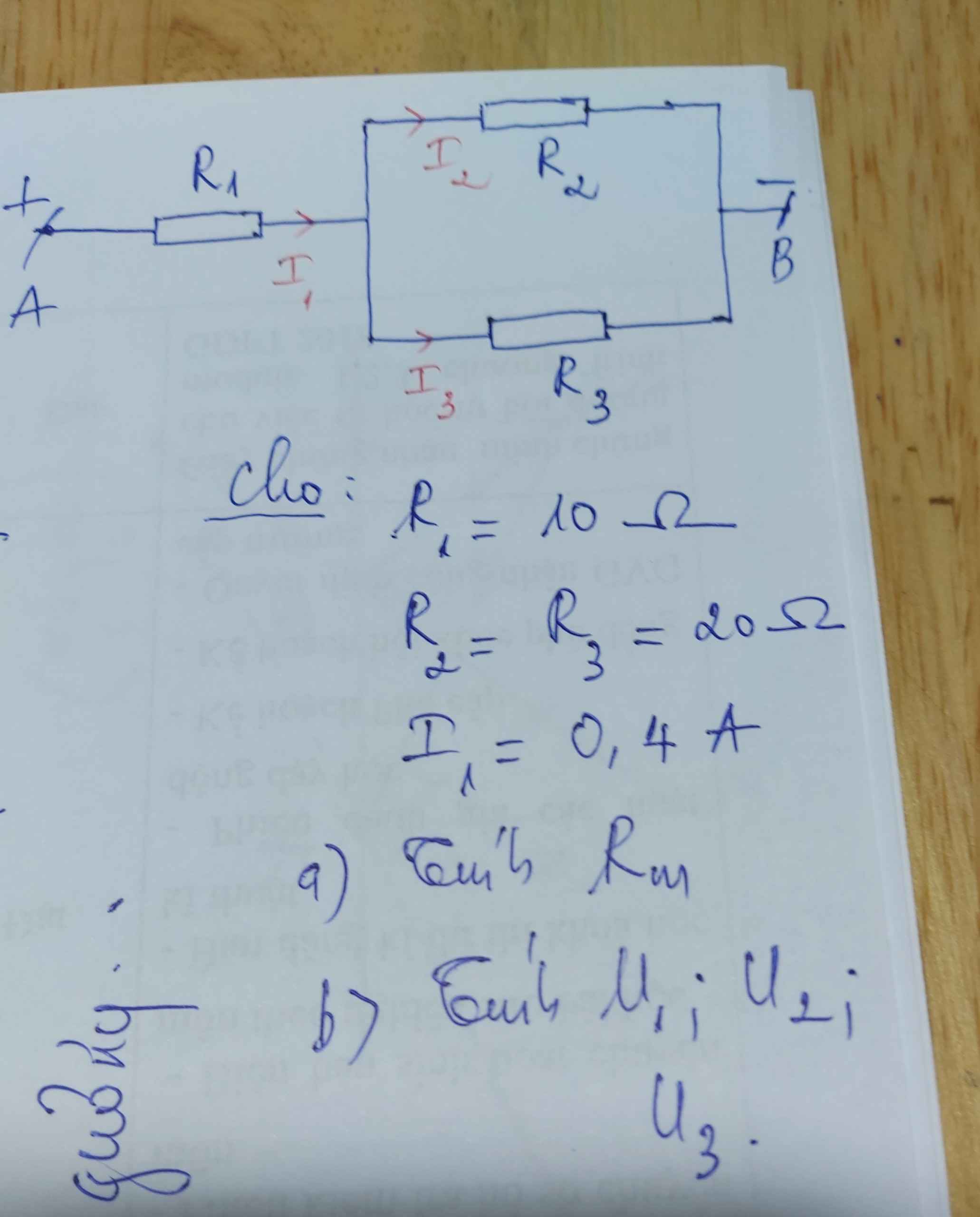
\(R_1nt\left(R_2//R_3\right)\)
a)\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot20}{20+20}=10\Omega\)
\(R_m=R_1+R_{23}=10+10=20\Omega\)
b)\(I_m=I_{23}=I_1=0,4A\)
\(U_1=R_1\cdot I_1=10\cdot0,4=4V\)
\(U_{23}=R_{23}\cdot I_{23}=10\cdot0,4=4V\)
Có \(R_2//R_3\Rightarrow U_2=U_3=U_{23}=4V\)
5 tháng 11 2021
\(R_m=R_1+\dfrac{R_2.R_3}{R_2+R_3}=10+\dfrac{20.20}{20+20}=20\left(\Omega\right)\)
\(I=I_1=I_{23}=0,4\left(A\right)\)
\(U_1=I_1.R_1=0,4.10=4\left(V\right)\)
\(U_{23}=U_2=U_3=I_{23}.R_{23}=0,4.\dfrac{20.20}{20+20}=4\left(V\right)\)