chứng minh x1+x2+x3+........+xm/y1+y2+y3+.......+ym=q/p
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 1 2015
Có vẻ như giữa (x2p - y2q)2n và (x3p - y3q)2n thiếu dấu + thì phải?
Ta có thể chứng minh như sau:
Với mọi n thuộc tập N*, ta có: k2n >= 0 với mọi k. (1)
-> (x1p - y1q)2n + ... + (xmp - ymq)2n luôn bằng 0
-> x1p - y1q = 0, x2p - y2q = 0, ... và xmp - ymq = 0 (2)
Giả sử điều cần chứng minh là đúng: (x1 + ... + xm) / (y1 + ... + ym) = q / p
-> p*(x1 + ... + xm) = q*(y1 + ... + ym)
-> x1p + ... + xmp = y1q + ... + ymq
-> (x1p - y1q) + ... (xmp - ymq) = 0 (3)
Theo (2), (3) luôn đúng -> Giả sử của ta là chính xác.
11 tháng 12 2022
x1-x2=3(x3-x2+672)
=>x1-x2=3x3-3x2+2016
=>x1+2x2-3x3=2016
3(y2+y3)=y1+5(y2-403)
=>3y2+3y3-y1-5y2+2015=0
=>-y1-2y2+3y3=-2015
=>y1+2y2-3y3=2015
Vì x,y tỉ lệ thuận
nên x1/y1=x2/y2=x3/y3
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_3}{y_3}=\dfrac{x_1+2x_2-3x_3}{y_1+2y_2-3y_3}=\dfrac{2016}{2015}\)
=>x=2016/2015y
=>y=2015/2016x
CM
29 tháng 1 2019
Chọn C.
Gọi 
Khi đó phương trình tiếp tuyến
M
0
là
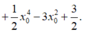
Ta có: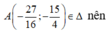 
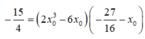
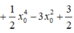
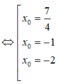
Không mất tính tổng quát của M 1 ( x 1 ; y 1 ) , M 2 ( x 2 ; y 2 ) , M 3 ( x 3 ; y 3 ) , ta có:
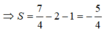
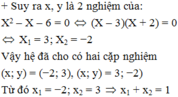
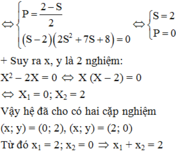
Đề không cho thêm gì à bạn? thththtt