Cho a.b,c là các số thực thỏa mãn 0<a,b,c<1 và ab+bc+ca=1.
Tìm GTNN của P=\(\frac{a^2\left(1-b\right)}{b}+\frac{b^2\left(1-c\right)}{c}+\frac{c^2\left(1-a\right)}{a}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 2 2019
Đáp án B
Đặt log 9 x = log 12 y = log 16 x + y = t ⇔ x = 9 t y = 12 t và x + y = 16 t
Suy ra 9 t + 12 t = 16 t ⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 ⇔ 3 4 t 2 + 3 4 t − 1 = 0 ⇔ 3 4 t = − 1 + 5 2
Vậy x y = 9 t 12 t = 3 4 t = − 1 + 5 2 = − a + b 2 ⇔ a = 1 b = 5 ⇒ P = a b = 5
T
24 tháng 9 2015
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).Vậy điều giả sử trên là sai,
a,b,c là 3 số dương.
24 tháng 9 2015
Giả sử a<0,vì abc>0 nên bc<0.Mặt khác thì ab+ac+bc>0<=>a(b+c)>-bc>0=>a(b+c)>0,mà a<0 nên b+c<0=>a+b+c<0(vô lý).
Vậy điều giả sử trên là sai,
Do đó a,b,c là 3 số dương.
CM
4 tháng 2 2019
Đáp án D
Từ x + y = 5 4 ⇒ y = 5 4 - x vì y > 0 ⇒ 0 < x < 5 4 ⇒ S = 4 x + 1 5 - 4 x ∀ x ∈ 0 ; 5 4
Xét f ( x ) = 4 x - 1 5 - 4 x
f ' ( x ) = 0 ⇔ - 4 x 2 + 4 5 - 4 x 2 = 0 ⇒ x = 1 ∈ 0 ; 5 4
Bảng biến thiên:
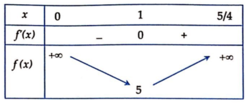
⇒ m i n S = m i n 0 ; 5 4 f ( x ) = 5 khi x = 1 y = 1 ⇒ a . b = 1 4