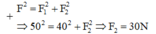Cho lực vec tơ F có độ lớn F = 10 N, phân tích vec tơ F thành hai lực vec tơ F1 và F2 trên hai trục tọa độ Oxy vuông góc nhau, biết góc giữa vec tơ F và Ox là 60°. Tìm độ lớn của F1 và F2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



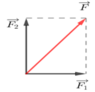
Ta có:
F 1 → ⊥ F 2 → ⇒ F 2 = F 1 2 + F 2 2 ⇒ F 2 = F 2 − F 1 2 = 100 2 − 60 2 = 80 N
Đáp án: A

Đáp án A
Vì F 2 = F 1 2 + F 2 2
⇒ 50 2 = 40 2 + F 2 2 ⇒ F 2 = 30 N

a) Đúng
Giải thích: Nhận thấy a→ = -3.i→
Vì –3 < 0 nên a→ và i→ ngược hướng.
b) Đúng.
Giải thích:
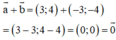
⇒ a→ = -b→ nên a→ và b→ là hai vec tơ đối nhau.
c) Sai
Giải thích:
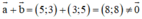
⇒ a→ ≠ -b→ nên a→ và b→ không phải là hai vec tơ đối nhau.
d) Đúng
Nhận xét SGK : Hai vec tơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

F2 = \(\sqrt{F^2-F_{1^{ }}^2}\)= \(\sqrt{10000-3600}=\sqrt{6400}=80N\)

Chiếu lên trục toạ độ
\(\Rightarrow F_1=F.\cos60=\frac{10.1}{2}=5\left(N\right)\)
\(\Rightarrow F_2=F.\sin60=\frac{10.\sqrt{3}}{2}=5\sqrt{3}\left(N\right)\)