Cho hình bình hành ABCD tâm O . Hãy tính các véc tơ sau theo \(AB^{\rightarrow}\)và \(AD^{\rightarrow}\)
a)\(AI^{\rightarrow}\) với I là trung điểm của BO
b) \(BG^{\rightarrow}\)với G là trọng tâm Δ OCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Mệnh đề \(P \Rightarrow Q\): “Nếu tứ giác ABCD là hình bình hành thì nó có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.
Mệnh đề này đúng vì “hai đường chéo cắt nhau tại trung điểm của mỗi đường” là tính chất của hình hình hành.
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\), được phát biểu là: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì nó là hình bình hành”.

a, Ta có:AM+AN=OM-OA+ON-OA=OM+ON+AC=OC+AC=3/2OC
GA+3GB+GC+OD=2GB+OD=OB+OD=0
C,

a) Vì tam giác AFB đồng dạng với ACF(g.g) nên:
AF/AC=AB/AF hay AF^2=AB.AC => AF=căn(AB.AC) ko đổi 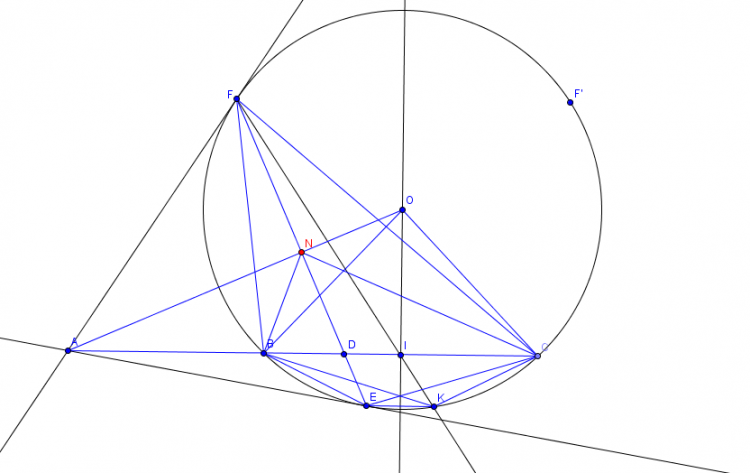
Mà AE=AF (T/cTtuyen) nên E, F cùng thuộc đường tròn bán kính căn(AB.AC)
b)Ta có: OI vuông góc với BC (T/ đường kính và dây)
Các điểm E, F, I cùng nhìn OA dưới 1 góc ko đổi 90 độ nên O,I,F,A,E cùng thuộc đường tròn đường kính OA
Ta có góc FIA=FOA(Cùng chắn cung FA trong đường tròn (OIFAE)
Mà góc FKE=FOA( Cùng bằng \(\frac{1}{2}\) góc FOE)
Suy ra góc FIA=FKE, nhưng hai góc này lại ở vị trí SLT nên KE//AB

IJ là đường trung bình của hình thang \(\Rightarrow\left\{{}\begin{matrix}IJ||AB\\IJ=\dfrac{AB+CD}{2}\end{matrix}\right.\)
Qua G kẻ đường thẳng song song AB lần lượt cắt SB, SA tại E và F
\(\Rightarrow\) Tứ giác IJEF là thiết diện của (GIJ) và chóp
\(EF||AB||IJ\Rightarrow IJEF\) là hình thang
Gọi M là trung điểm AB
Theo tính chất trọng tâm và định lý Talet:
\(\dfrac{EF}{AB}=\dfrac{SG}{SM}=\dfrac{2}{3}\)
Để IJEF là hình bình hành \(\Leftrightarrow IJ=EF\)
\(\Leftrightarrow\dfrac{2}{3}AB=\dfrac{AB+CD}{2}\Leftrightarrow\dfrac{1}{3}AB=CD\)
\(\Rightarrow AB=3CD\)

\(\left\{{}\begin{matrix}\overrightarrow{MN}=\overrightarrow{AB}\\\overrightarrow{MN}=\overrightarrow{DC}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\) ABCD là hbh