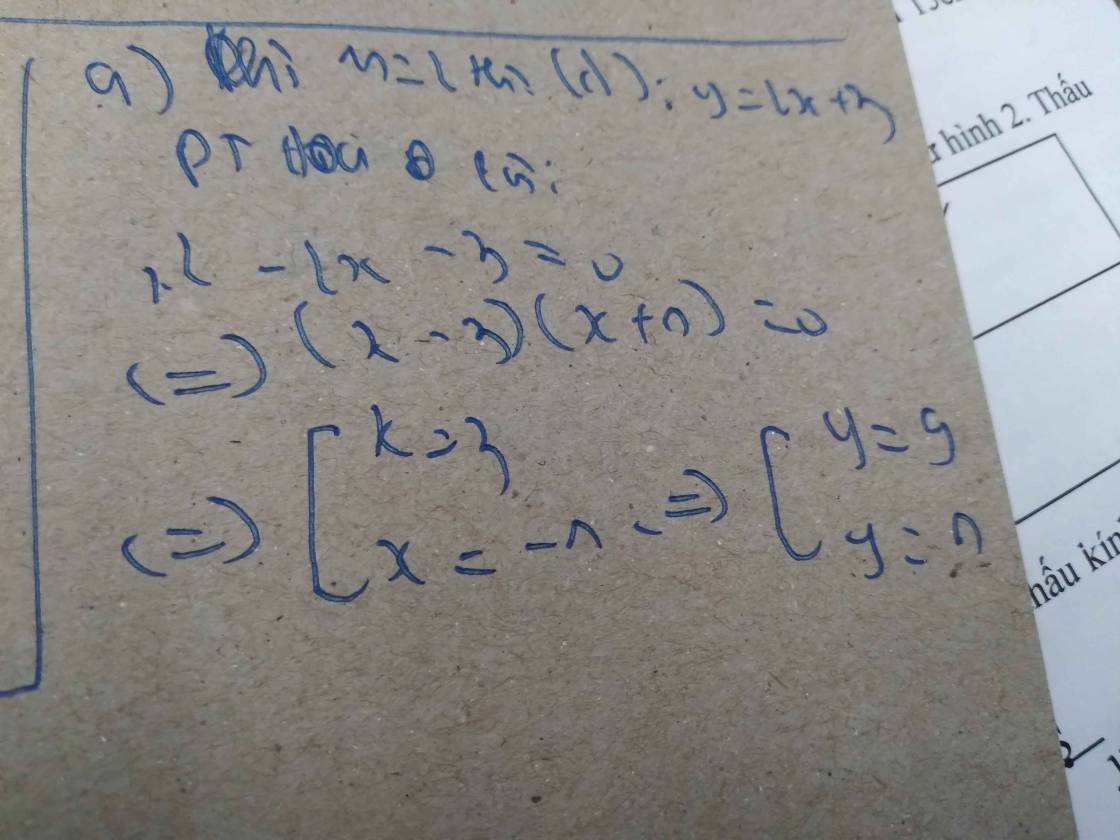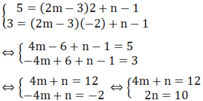cho (d): mx-y=2 và (d'): (2-m)x+y=m. Tìm giao điểm của (d) và (d') với m=2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
11 tháng 5 2021
HĐ g/đ là nghiệm pb
`x^2=mx-4`
`<=>x^2-mx+4=0`
(d) tiếp xúc (p)
`<=>` pt có nghiệm kép
`=>\Delta=0`
`<=>m^2-16=0`
`<=>` $\left[ \begin{array}{l}m=4\\m=-4\end{array} \right.$
CM
30 tháng 5 2019
Đáp án B
+ Tọa độ giao điểm của hai đường thẳng d và d’ là nghiệm của hệ phương trình:
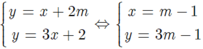
suy ra d và d’ cắt nhau tại M( m-1; 3m-1)
+ Vì ba đường thẳng d; d’ ; d’’ đồng quy nên d’’ qua M ta có
3m-1= -m( m-1) + 2 hay m2+ 2m-3=0
Suy ra m=1 hoặc m= -3
Với m= 1 ta có ba đường thẳng là d: y= x+ 2; d’ : y= 3x+ 2 và d’’: y= -x+ 2 phân biệt và đồng quy tại M(0; 2).
Với m= -3 ta có d và d’’ trùng nhau suy ra m= -3 không thỏa mãn
Vậy m= 1 là giá trị cần tìm.
Chọn B.
30 tháng 11 2023
Phương trình hoành độ giao điểm là:
\(x^2-3x+2=mx+2\)
=>\(x^2-3x+2-mx-2=0\)
=>\(x^2+x\left(-m-3\right)=0\)
\(\Delta=\left(-m-3\right)^2-4\cdot1\cdot1=\left(m+3\right)^2-4=\left(m+3-2\right)\left(m+3+2\right)=\left(m+1\right)\left(m+5\right)\)
Để (P) tiếp xúc với (d) thì Δ=0
=>(m+1)(m+5)=0
=>\(\left[{}\begin{matrix}m+1=0\\m+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-5\end{matrix}\right.\)
16 tháng 6 2023
(d): VTPT là (m;1)
(d'): VTPT là (m;-4)
(d) vuông góc (d')
=>m^2-4=0
=>m=2 hoặc m=-2
=>Có 2 số nguyên m thỏa mãn
21 tháng 3 2023
a: Khi m=4 thì y=4x-4
b: PTHDGĐ là:
x^2-mx+4=0
Δ=(-m)^2-4*1*4=m^2-16
Để (P) tiếpxúc với(d) thì m^2-16=0
=>m=4 hoặc m=-4
AH
Akai Haruma
Giáo viên
19 tháng 4 2021
Lời giải:
PT hoành độ giao điểm:
$2x^2-mx-1=0(*)$
$\Delta=m^2+8>0$ với mọi $m$ đồng nghĩa $(P)$ và $(d)$ luôn cắt nhau tại 2 điểm $A,B$ phân biệt với mọi $m$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_A+x_B=\frac{m}{2}\\ x_Ax_B=-\frac{1}{2}\end{matrix}\right.\)
Khoảng cách từ $O$ đến $AB$ là:
$\frac{|m.0+1-0|}{\sqrt{m^2+1}}=\frac{1}{\sqrt{m^2+1}}$
$AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}$
$=\sqrt{(x_A-x_B)^2+(mx_A+1-mx_B-1)^2}$
$=\sqrt{(x_A-x_B)^2(m^2+1)}$
$=\sqrt{(x_A+x_B)^2-4x_Ax_B}.\sqrt{m^2+1}$
$=\sqrt{\frac{m^2}{4}+2}.\sqrt{m^2+1}$
$S_{OAB}=\frac{1}{2}\sqrt{\frac{m^2}{4}+2}.\sqrt{m^2+1}.\frac{1}{\sqrt{m^2+1}}=\frac{3m}{2}$
$m=\pm \sqrt{\frac{8}{35}}$
