Cho đoạn thẳng AB = 4cm . Trên nửa mặt phẳng có bờ chứa đường thẳng AB lấy điểm M sao cho \(\widehat{AMB}=90\) . Kẻ \(MH\perp AB\left(H\in AB\right)\) . Tìm vị trí của điểm H sao cho diện tích tam giác AMH lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 3 2019
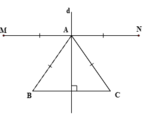
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN
23 tháng 8 2019
Chắc mk nghĩ thế này là ổn lắm rùi
Hội con 🐄 chúc bạn học tốt!!!
LS
21 tháng 2 2018
a)
Vì M thuộc AB nên AM + MB = AB |
|
Có AN = AM |
Do N thuộc tia đối của tia AB nên điểm A nằm giữa N và B |
BN = AB + AN = 5 + 3 = 8 cm |
AM + 2 = 5 
AM = 3 cmb)
+ Trên cùng một nửa mặt phẳng có bờ chứa tia AB có: |
hay |
+ Trên cùng một nửa mặt phẳng có bờ AB, ta có
|
hay |
và 
là hai góc kề bù .
c)
Vì BN = AB + AN = 5 + AN Suy ra BN có độ dài lớn nhất khi AN có độ dài lớn nhất |
Mà AN = AM |
Có AM |
Vậy khi điểm M trùng với điểm B thì BN có độ dài lớn nhất. |
cho mình bổ sung tí là trên cạnh AB nha