Nguyên tử của nguyên tố B có tổng số hạt cơ bản là 49, trong đó số hạt ko mang điện bằng 53,125% số hạt mang điện . Biết rằng khối lượng mol của B có giá trị bằng số khối của B. Tổng khối lượng các hạt electron có trong 26,4 g B là?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2021
\(1/\\ Tổng: 2p+n=49(1)\\ \text{Hạt không mang điện bằng 53,125% số hạt mang điện: }\\ n=2.53,125\%p\\ \to -1,0625p-n=0(2)\\ (1)(2)\\ p=e=16\\ n=17\\ A=16+17=33 (S)\\ \)
4 tháng 10 2021
\(Tổng: 2p+n=36(1)\\ \text{Số hạt mang điện gấp đôi số hạt không mang điện là 36: }\\ 2p=2n\\ \to p-n=0(2)\\ (1)(2)\\ p=e=n=12\\ A=12+12=24(Mg)\)
20 tháng 5 2017
Giả sử số hiệu nguyên tử, số nơtron trong nguyên tử của nguyên tố X lần lượt là Z, N.
Ta có hpt:
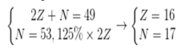
→ Điện tích hạt nhân của X là 16+
→ Chọn D.
27 tháng 9 2021
Theo đề bài, ta có: \(2Z+N=49\left(1\right)\)
\(N=53,125\%.2Z\Leftrightarrow1,0625Z-N=0\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}Z=16\\N=17\end{matrix}\right.\Rightarrow A=Z+N=16+17=33\)
\(\Rightarrow KHNT:^{16}_{33}S\)
28 tháng 9 2021
thật ra em đang viết sai, số khối viết trên, số hiệu nguyên tử viết dưới
DH
28 tháng 2 2021
a, Gọi số proton, electron và notron của X lần lượt là p;e;n
Theo gt ta có:
\(\left\{{}\begin{matrix}2p+n=34\\2p-n=10\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}p=11\\n=12\end{matrix}\right.\)
Vậy X là Na
b, Ta có: $m_{Na}=23.1,9926.10^{-23}:12=3,819.10^{-23}$
TP
27 tháng 7 2021
Theo đề ta có : \(\left\{{}\begin{matrix}2Z+N=49\\N=53,125\%.2Z\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}Z=16=P=E\\N=17\end{matrix}\right.\)
Tổng số các loại hạt proton, nơtron và electron của X là 49
p + n + e = 49 => 2p + n = 49 (1)
Tổng số hạt không mang điện bằng 53,125% số hạt mang điện
n = 53,125% (p+e) hay n = 53,125%.2p (2)
Từ (1), (2) ta có p = e = 16 , n =17
Đến đây tự tính nhé