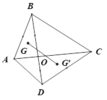
cho tứ giác ABCD, O là giao điểm , O là giao 2 đường chéo AC,BD Gọi G theo thứ tự là trọng tâm tam giác OAB và OCD. Biểu diễn \(\overrightarrow{GG'}\) theo \(\overrightarrow{AC}\) và \(\overrightarrow{BD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 4 2017
Chọn D.
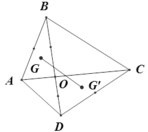
+ Vì G’ là trọng tâm của tam giác OCD nên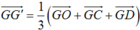 
. (1)
+ Vì G là trọng tâm của tam giác OAB nên: 
(2)
+ Từ (1) và (2) suy ra: 
18 tháng 3 2016
Đặt \(\overrightarrow{u}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OH}\)
Ta sẽ chứng minh \(\overrightarrow{u}=\overrightarrow{O}\)
Gọi A1, B1, C1 theo thứ tự là hình chiếu của A, B, C ( cũng là hình chiếu của H) trên các đường thẳng BC, CA, AB và gọi Ao, Bo, Co theo thứ tự là trung điểm BC, CA, AB (như hình vẽ)
Chiếu vectơ \(\overrightarrow{u}\) lên đường thẳng BC theo phương của \(\overrightarrow{AH}\) ta được
\(\overrightarrow{u_a}=\overrightarrow{A_oA_1}+\overrightarrow{A_oB}+\overrightarrow{A_oC}-\overrightarrow{A_oA_1}=\overrightarrow{O}\)
Suy ra \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{AH}\) (1)
Tương tự như vậy,
ta cũng có \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{BH,}\overrightarrow{CH}\) (2)
Từ (1) và (2) và do các vectơ \(\overrightarrow{AH,}\), \(\overrightarrow{BH},\overrightarrow{CH}\) đôi một không cùng phương suy ra \(\overrightarrow{u}=\overrightarrow{O}\)
Vậy \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
Nhưng \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\) nên \(\overrightarrow{OH}=3\overrightarrow{OG}\)
Do đó G, H, O thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{BM}\right)+\left(\overrightarrow{NC}+\overrightarrow{ND}\right)\)
\(=2\overrightarrow{MN}\)
\(\Rightarrow\) A đúng nên D sai
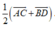
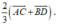
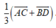
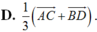
Xét 2 tam giác ABC và A'B'C' bất kì.
Có: \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\left(\overrightarrow{AG}+\overrightarrow{GA'}\right)+\left(\overrightarrow{BG}+\overrightarrow{GB'}\right)+\left(\overrightarrow{CG}+\overrightarrow{GC'}\right)\)
\(=\overrightarrow{0}+\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)=3\overrightarrow{GG'}\)
Áp dụng có:
\(\overrightarrow{OO}+\overrightarrow{AC}+\overrightarrow{BD}=3\overrightarrow{GG'}\)
\(\Leftrightarrow\overrightarrow{GG'}=\frac{1}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}\)
#Walker