Cho hình thang ABCD có đáy AB=a, CD =2a. Gọi M,N lần lượt là trung điểm AD và BC. Tính độ dài của vecto MN+ vecto BD + vecto CA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P

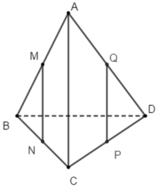
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và
M
N
=
1
2
A
C
(1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và Q P = 1 2 A C (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)

Đáp án C

hình bạn tự vẽ nha
ta có MN lần lượt là trung điểm của AD và BC
=> MN là đường tb trong ht ABCD
=>MN=\(\frac{AB+DC}{2}\)(1)=>2MN=AB+AC hay \(2\overrightarrow{MN}=\overrightarrow{AB}+\overrightarrow{DC}\)
ta lại có\(\overrightarrow{BD}+\overrightarrow{CA}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{CD}+\overrightarrow{DA}=-\left(\overrightarrow{AB}+\overrightarrow{DC}\right)=-2\overrightarrow{MN}\)
khi đó \(\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}=\overrightarrow{MN}-2\overrightarrow{MN}=-\overrightarrow{MN}\) =>\(\left|\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}\right|=\left|-\overrightarrow{MN}\right|=MN\)
từ (1) =>MN=\(\frac{a+2a}{2}=\frac{3a}{2}\)


Do MN là đường trung bình hình thang nên \(\overrightarrow{MN}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{DC}\right)\)
Mà \(CD=2AB\Rightarrow\overrightarrow{DC}=2\overrightarrow{AB}\Rightarrow\overrightarrow{MN}=\frac{3}{2}\overrightarrow{AB}\)
Ta có: \(\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}=\frac{3}{2}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{BA}\)
\(=\frac{3}{2}\overrightarrow{AB}-\overrightarrow{DC}-\overrightarrow{AB}=\frac{3}{2}\overrightarrow{AB}-2\overrightarrow{AB}-\overrightarrow{AB}=-\frac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\left|\overrightarrow{MN}+\overrightarrow{BD}+\overrightarrow{CA}\right|=\left|-\frac{3}{2}\overrightarrow{AB}\right|=\frac{3}{2}AB=\frac{3a}{2}\)