Cho tứ giác ABCD có góc A=góc D=90 độ,góc C=40 độ.AB=4cm,AD=3cm Tính diện tích tứ giác ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2015
kẻ đường cao BH
xét tứ giác ABHD có góc A=góc D=góc H=90 độ
=> ABHD là hình chữ nhật
=> S ABHD=AB.AD=4.3=12 cm vuông
xét tam giác vuông BHC có tanC=BH/HC =>HC=BH/tanC=3/tan\(40^0\)=3.6 cm
=> S BHC=1/2.BH. HC=1/2.3.3,6=5,4 cm vuông
=> S ABCD= S ABHC+S BHC=12+5,4=17,4 cm vuông
NT
2
19 tháng 8 2017
kẻ đường cao BH
xét tứ giác ABHD có góc A=góc D=góc H=90 độ
=> ABHD là hình chữ nhật
=> S ABHD=AB.AD=4.3=12 cm vuông
xét tam giác vuông BHC có tanC=BH/HC =>HC=BH/tanC=3/tan400=3.6 cm
=> S BHC=1/2.BH. HC=1/2.3.3,6=5,4 cm vuông
=> S ABCD= S ABHC+S BHC=12+5,4=17,4 cm vuông
NT
24 tháng 7 2015
Tứ giác ABCD có góc A= góc D = 90 độ nên ABCD là hình thang vuông. Từ B kẻ BH vuông góc với CD. Ta có BH= AD =3 cm.
Xét tam giác vuông BHC có góc C=40 độ nên tan 40 = BH/HC . suy ra HC = BH/tan40 = 3/ tan 40
Ta lại có AB= DH =4 cm nên CD = DH+HC 4+ 3/ tan 40
Vậy diện tích tứ giác ABCD = (AB+CD).BH/2
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 9 2021
1.
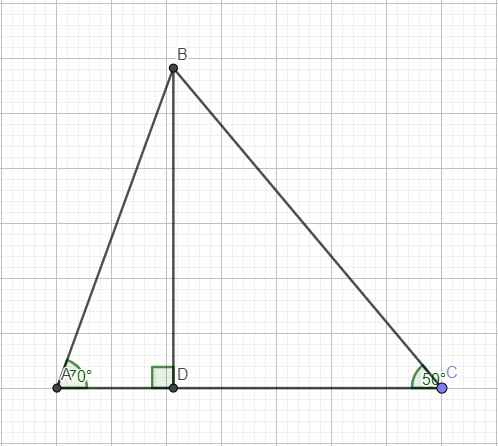
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
