Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O). Gọi E,F là chân các đường cao hạ từ B và C; M là trung điểm BC, EF cắt đường tròn (O) tại hai điểm S,T; SM cắt (O) lần thứ hai ở K. Chứng minh rằng AK vuông góc với HT.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2023
1: góc AFB=góc AEB=góc ADB=90 độ
=>A,F,B,E,D cùng nằm trên 1 đường tròn
2: Xét ΔAFE và ΔACM có
góc FAE chung
góc AFE=góc ABE=góc ADE=góc MCA
=>ΔAFE đồng dạng với ΔACM
=>AE/AM=AF/AC
=>AM/AC=AE/AF
góc FAB=góc ACB
=>góc FBA=90 độ-góc ACB=góc EBC
30 tháng 6 2021
A B C H D M E F P Q R S K I T O
Gọi I,T lần lượt là trung điểm HF, EF. Ta có \(\Delta FHD~\Delta FEC\)(g.g), trung tuyến tương ứng là DI,CT
Suy ra \(\widehat{ECT}=\widehat{HDI}\). Vì DI là đường trung bình \(\Delta HMF\) nên \(\widehat{HDI}=\widehat{HMF}=\widehat{ACQ}\)
Do đó \(\widehat{ECT}=\widehat{ACQ}\), suy ra C,T,Q thẳng hàng. Tương tự B,T,P thẳng hàng.
Mặt khác, theo một kết quả quen thuộc thì tứ giác EHFR điều hòa, suy ra RH là đường đối trung của \(\Delta REF\)
Lại có HS || EF vì cùng vuông góc OA. Suy ra (HF = (SE hay H,S đẳng giác trong \(\widehat{ERF}\)
Suy ra RS là trung tuyến của \(\Delta REF\) hay RS đi qua T.
Vậy RS,BP,CQ cùng đi qua T.
4 tháng 8 2019
A B C M N D E
Ta có ^MEN = ^NBD + ^MCD = 1800 - ^MAN. Suy ra tứ giác AMEN nội tiếp
Cũng dễ có tứ giác BCMN nội tiếp đường tròn (BC)
Từ đó ^AEM = ^ANM = ^MCB = ^MCD = 1800 - ^MED. Hay ^AEM + ^MED = 1800
Vậy thì A,E,D thẳng hàng (đpcm).
KN
27 tháng 2 2020
Ta có ^BCN = ^BMN ( do tứ giác BNMC nội tiếp )
=> ^NBC = ^AMN ( cùng phụ với hai góc bằng nhau ) (1)
Mặt khác do BDEN và CDEM là các tứ giác nội tiếp chung cạnh DE
Nên ^NBD + ^MCD = ^NEM ( tính chất góc ngoài tứ giác nội tiếp )
Mà ^NBD + ^MCD + ^NAM = 1800
Suy ra ^NEM + ^NAM = 1800 . Vây AMEN nội tiếp
Do đó: ^AMN = ^AEN (2)
Từ (1) và (2) suy ra ^NBD = ^AEN
Mà ^NBD + ^DEN = 1800 (do BDEN nội tiếp)
Nên ^DEN + ^AEN = 1800 => ^AED=1800 .
Vậy ba điểm A, E, D thẳng hàng (đpcm)
CM
13 tháng 7 2019
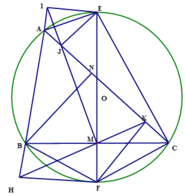
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)
A B C H E F S T M K' K O G L N
* Bổ đề 1: Xét tam giác ABC có trực tâm H, tâm ngoại tiếp O và đường tròn Euler \(\left(\omega\right)\). Một đường thẳng \(\Delta\)đi qua H và cắt \(\left(\omega\right)\);(O) lần lượt tại I,K. Khi đó I là trung điểm của HK. (Các bạn tự chứng minh)
* Bổ đề 2: Xét tam giác ABC cân tại A. Điểm M thỏa mãn ^AMB = ^AMC. Khi đó AM là trung trực của BC.
* Giải bài toán: Kẻ đường thẳng qua A vuông góc với HT, đường thẳng này cắt (O) tại K' khác A.
Gọi M là trung điểm BC, HT cắt đường tròn (MEF) và (O) lần lượt tại G và L (G thuộc cung FM nhỏ)
Do (MEF) là đường tròn Euler-9 điểm của \(\Delta\)ABC nên áp dụng Bổ đề 1 ta thu được GH = GL
Đồng thời, kết hợp với ĐL Reim ta cũng suy ra tứ giác GFTC nội tiếp
Từ đây ^CGH = ^HFE = ^CBH. Suy ra ^BCG = ^BHG = ^THE = ^CAK' = ^CBK' và ^BGC = ^CK'B (= 1800 - ^BAC)
Suy ra tứ giác CK'BG là hình bình hành. Từ đó GK',BC,HN cùng đi qua điểm M
Do vậy tứ giác GLNK' là hình bình hành (Vì GH = GL và cùng song song với NK')
Dẫn đến K'G = NL = K'T, suy ra AG = AT = AS (Vì AK' là trung trực của GT)
Ta thấy \(\Delta\)ASG cân tại A (cmt); ^ALS = ^ALG (Vì (AS = (AT ). Theo Bổ đề 2 thì AL vuông góc SG (1)
Ta lại có AL vuông góc LN; LN // GK' nên AL vuông góc GK' (2)
Từ (1) và (2) suy ra hai đường thẳng SG, GK' trùng nhau hay SM đi qua K'
Như vậy K' trùng K, đồng nghĩa với việc AK vuông góc với HT (đpcm).
chúc mừng đạt lần nữa nhen