Tìm m để pt sin2x-2sinx-m=0 có nghiệm thuộc (-π/4;π/6).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án B
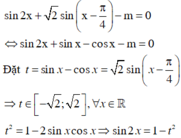
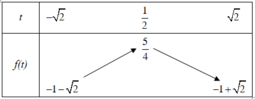
Ta đi tìm m để phương trình 1 − t 2 + t − m = 0 có nghiệm t ∈ − 2 ; 2

Vậy phương trình đã cho có nghiệm ⇔ m = f t có nghiệm trên − 2 ; 2
⇔ m ∈ − 1 − 2 ; 5 4 mà m ∈ ℤ ⇒ m ∈ − 2 ; − 1 ; 0 ; 1
Vậy có 4 giá trị m thỏa mãn.

\(\Leftrightarrow2sinx=4-2m\)
\(\Leftrightarrow sinx=\dfrac{4-2m}{2}\)
ĐK có nghiệm \(-1\le\dfrac{4-2m}{2}\le1\)
\(\Leftrightarrow-2\le4-2m\le2\)
\(\Leftrightarrow-6\le-2m\le-2\)
\(\Leftrightarrow3\ge m\ge1\)
\(\Leftrightarrow1\le m\le3\)
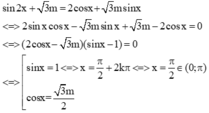

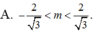

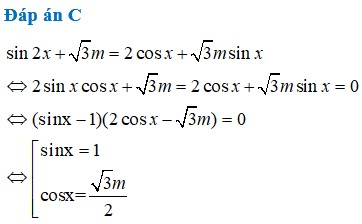
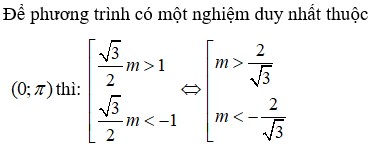
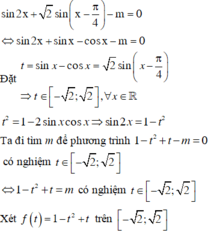

Đặt \(sinx=a\), do \(x\in\left(-\frac{\pi}{4};\frac{\pi}{6}\right)\Rightarrow a\in\left(-\frac{\sqrt{2}}{2};\frac{1}{2}\right)\)
Bài toán trở thành tìm m để \(a^2-2a-m=0\) có nghiệm thuộc \(\left(-\frac{\sqrt{2}}{2};\frac{1}{2}\right)\)
\(\Leftrightarrow f\left(a\right)=a^2-2a=m\)
\(f'\left(a\right)=2a-2=0\Rightarrow a=1\)
\(\Rightarrow f\left(a\right)\) nghịch biến trên \(\left(-\frac{\sqrt{2}}{2};\frac{1}{2}\right)\Rightarrow f\left(\frac{1}{2}\right)< f\left(a\right)< f\left(-\frac{\sqrt{2}}{2}\right)\)
\(\Rightarrow-\frac{3}{4}< f\left(a\right)< \frac{1+2\sqrt{2}}{2}\)
\(\Rightarrow-\frac{3}{4}< m< \frac{1+2\sqrt{2}}{2}\)