Cho hình thoi ABCD cạnh a và góc BCD = 60*. O là tâm hình thoi. Tính \(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|,\left|\overrightarrow{OB}-\overrightarrow{DC}\right|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
\(\left|\overrightarrow{OA}-\overrightarrow{CB}\right|=\left|\overrightarrow{OA}+\overrightarrow{BC}\right|=\left|\overrightarrow{OA}+\overrightarrow{AD}\right|=\left|\overrightarrow{OD}\right|=OD=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\)
\(\left|\overrightarrow{AB}+\overrightarrow{DC}\right|=\left|\overrightarrow{AB}+\overrightarrow{AB}\right|=2\left|\overrightarrow{AB}\right|=2AB=2a\)
\(\left|\overrightarrow{CD}-\overrightarrow{DA}\right|=\left|\overrightarrow{CD}+\overrightarrow{AD}\right|=\left|\overrightarrow{BA}+\overrightarrow{AD}\right|=\left|\overrightarrow{BD}\right|=BD=a\sqrt{2}\)
HP
26 tháng 1 2021
Gọi N là trung điểm BC
\(\left|\overrightarrow{MA}+\overrightarrow{MC}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MO}+2\overrightarrow{MB}+2\overrightarrow{OC}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow\left|2\overrightarrow{MC}+2\overrightarrow{MB}\right|=\left|\overrightarrow{AB}-\overrightarrow{AD}\right|\)
\(\Leftrightarrow4\left|\overrightarrow{MN}\right|=\left|\overrightarrow{BD}\right|\)
\(\Rightarrow\left|\overrightarrow{BD}\right|=4\left|\overrightarrow{MN}\right|=4\left|\overrightarrow{DN}+\overrightarrow{MD}\right|\ge4MD-4DN\)
\(\Rightarrow4MD\le BD+4DN\)
\(\Leftrightarrow MD\le\dfrac{BD+4DN}{4}=\dfrac{a\sqrt{2}+2a\sqrt{5}}{4}=\dfrac{2\sqrt{5}+\sqrt{2}}{4}a\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2019
a/ \(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}+\overrightarrow{OD}\right|=\left|\overrightarrow{0}+\overrightarrow{0}\right|=0\)
b/ \(\left|\overrightarrow{OA}+\overrightarrow{OB}\right|+\left|\overrightarrow{OC}+\overrightarrow{OD}\right|=a+a=2a\)
c/
\(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=\left|\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=2\left|\overrightarrow{OB}\right|=2\sqrt{a^2-\frac{a^2}{4}}=a\sqrt{3}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\Rightarrow |\overrightarrow p| = | \overrightarrow {AC}| =AC \)
+) \(\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow u| = | \overrightarrow {DB}| =DB\)
+) \(\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} \)\( = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
\(\Rightarrow |\overrightarrow v| = | \overrightarrow {DB}| =DB\)
+ Tính \(AC, DB\)
Tam giác ABD có \(AB=AD=a, \widehat A = 60^o\) nên nó là tam giác đều. Do đó DB = a.
Gọi O là giao điểm hai đường chéo.
Ta có: \(AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow AC = a \sqrt 3\)
Vậy \(|\overrightarrow p| = a \sqrt 3 ,|\overrightarrow u| = a, |\overrightarrow v| = a.\)
HP
16 tháng 12 2020
a, \(AC=\dfrac{AB}{sin45^o}=\dfrac{a}{\dfrac{\sqrt{2}}{2}}=a\sqrt{2}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cos\widehat{BAC}=a.a\sqrt{2}.cos45^o=a^2\)
b, \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=\overrightarrow{AC}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)\)
\(=\overrightarrow{AC}.\overrightarrow{BD}+\overrightarrow{AC}.\overrightarrow{BC}\)
\(=AC.BD.cos90^o+AC.AD.cos45^o\)
\(=a\sqrt{2}.a\sqrt{2}.0+a\sqrt{2}.a.\dfrac{\sqrt{2}}{2}=a^2\)
c, \(\overrightarrow{AB}.\overrightarrow{BD}=AB.BD.cos135^o=-a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=-a^2\)
d, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\left(2\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{BC}.\left(\overrightarrow{AD}+\overrightarrow{BD}\right)\)
\(=\overrightarrow{BC}.\overrightarrow{AD}+\overrightarrow{BC}.\overrightarrow{BD}\)
\(=AD^2+BC.BD.cos45^o\)
\(=a^2+a.a\sqrt{2}.\dfrac{\sqrt{2}}{2}=2a^2\)
e, \(\left(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\right)\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}\right)\)
\(=\left(\overrightarrow{AC}+\overrightarrow{AC}\right)\left(\overrightarrow{DB}+\overrightarrow{DB}\right)\)
\(=4.\overrightarrow{AC}.\overrightarrow{DB}=4.AC.DB.cos90^o=0\)
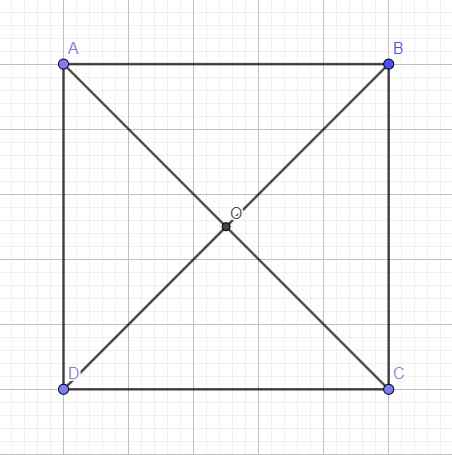
Tham khảo