cho tam giác abc , trực tâm h . biết hb = 3 , ha =7 tính Sabc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 5 2019
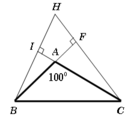
Vì H I A ^ + H F A ^ = 180 0 nên tứ giác HFAI nội tiếp.
Suy ra: I H F ^ + I A F ^ = 180 0 ⇒ I H F ^ = 180 0 − I A F ^ = 80 0
Ta có H A → , H B → = B H A ^ H B → , H C → = B H C ^ H C → , H A → = C H A ^
⇒ H A → , H B → + H B → , H C → + H C → , H A → = B H A ^ + B H C ^ + C H A ^
= 2 B H C ^ = 2.80 0 = 160 0
Chọn D.
CM
1 tháng 3 2017
Vì H là trực tâm tam giác ABC nên:
A H ⊥ C B ; B H ⊥ A C ; C H ⊥ B A ⇒ A H → . C B → = 0 ; B H → . A C → = 0 ; C H → . B A → = 0
Ta có
A H → . H B → − H C → + B H → . H C → − H A → + C H → . H A → − H B →
= A H → . C B → + B H → . A C → + C H → . B A → = 0
CHỌN B
23 tháng 7 2018
B
Theo bài ra, ta thấy: AM = 3 MH nên AH = 4 MH
BN = 3 NH nên BH = 4 NH
CQ = 3 QH nên CH = 4 QH
Suy ra: MH/AH = NH/BH (=1/4)
Do đó: MN song song với AB(định lí Ta-lét đảo)
MN /AB = MH/AH =1/4
Tương tự : NQ/BC = NH/BH =1/4 và MQ/AC = HQ/CH =1/4
Vì thế: MN/AB =NQ/BC = MQ/AC =1/4
Nên tam giác MNQ đồng dạng với tam giác ABC(c.c.c)
Tỉ số chu vi 2 tam giác = tỉ số 2 tam giác đồng dạng nên chu vi tam giác MNQ = 1/4 chu vi tam giác ABC
Vậy chu vi tam giác MNQ là 60:4 =15(cm)
2 tháng 8 2019
A B C E D F H I G
a) Qua H kẻ HG//AB cắt AC tại G; kẻ HI//AC cắt AB tại I như hình vẽ.
=> HI vuông BH ; CH vuông HG
và AIHG là hình bình hành
Xét tam giác BHI vuông tại H => BH<BI ( mối quan hệ cạnh góc vuông và cạnh huyền) (1)
Xét tam giác CHG vuông tại H => CH<CG
=> CH+BH + AH< BI+CG +AH
Ta lại có AH <AI+IH ( bất đẳng thức trong tam giác AIH)
mà IH=AG ( AIHG là hình bình hành theo cách vẽ )
=> AH < AI+AG
Vậy CH+BH+AH<BI+CG+AI+AG=AB+AC
b) Chứng minh AB+AC+BC>3/2 (HA+HB+HC)
Chứng minh tương tự như câu a.
Ta có: \(AB+AC>HA+HB+HC\)
\(BC+AC>HA+HB+HC\)
\(AB+BC>HA+HB+HC\)
Cộng theo vế ta có:
\(2AB+2AC+2BC>3HA+3HB+3HC\)
=> \(2\left(AB+AC+BC\right)>3\left(HA+HB+HC\right)\)
=> \(AB+AC+BC>\frac{3}{2}\left(HA+HB+HC\right)\)
TT
1
2 tháng 8 2019
Câu hỏi của Phạm Trung Kiên - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo nhé!
23 tháng 7 2023
a) Ta có: HA = 2RcosA HB = 2RcosB HC = 2RcosC AB = 2RsinC AC = 2RsinB Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2RsinC + 2RsinB Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < sinC + sinB Áp dụng bất đẳng thức tam giác, ta có: sinC + sinB > sin(A + B) = sinCOSA + cosCSINA = cosA + cosB Vậy ta có: cosA + cosB + cosC < sinC + sinB Do đó, ta có HA + HB + HC < AB + AC. b) Ta có: AB + BC + CA = 2R(sinA + sinB + sinC) = 2R(sinA + sinB + sin(A + B)) = 2R(2sin(A + B/2)cos(A - B/2) + sin(A + B)) = 4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B) Vậy ta cần chứng minh: 2RcosA + 2RcosB + 2RcosC < 2332 (4Rsin(A + B/2)cos(A - B/2) + 2Rsin(A + B)) Chia cả 2 vế cho 2R, ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) Áp dụng bất đẳng thức tam giác, ta có: sin(A + B) > sinC = sin(A + B/2 + B/2) = sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) Vậy ta có: 2sin(A + B/2)cos(A - B/2) + sin(A + B) < 2sin(A + B/2)cos(A - B/2) + sin(A + B/2)cos(B/2) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + cos(A + B/2)sin(B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2)) + sin(B/2)cos(A + B/2) = sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2)) Vậy ta có: cosA + cosB + cosC < 1166(2sin(A + B/2)cos(A - B/2) + sin(A + B)) < 1166(sin(A + B/2)(2cos(A - B/2) + cos(B/2) + cos(A + B/2))) Do đó, ta có HA + HB + HC < 2332(AB + BC + CA).