Chứng minh rằng : (a+b)2=a2+2.a.b+b2. B) (a-b)2=a2-2.a.b+b2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,a^2+b^2=\left(a+b\right)^2-2ab=9^2-2\cdot20=41\\ b,a^4+b^4=\left(a^2+b^2\right)^2-2a^2b^2=41^2-2\left(ab\right)^2\\ =1681-2\cdot400=881\\ c,\left(a-b\right)^2=a^2+b^2-2ab=41-2\cdot20=1\\ \Rightarrow a-b=1\\ \Rightarrow C=a^2-b^2=\left(a-b\right)\left(a+b\right)=9\cdot1=9\)

Biến đổi vế trái ta có:
VT = (a + b)( a 2 – ab + b 2 ) + (a – b)( a 2 + ab + b 2 )
= a 3 + b 3 + a 3 – b 3 = 2 a 3 = VP
Vế trái bằng vế phải nên đẳng thức được chứng minh.

z 2 = ( a + b i ) 2 = a 2 − b 2 + 2abi
( z ) 2 = ( a - b i ) 2 = a 2 − b 2 − 2abi
z.z− = (a + bi)(a − bi) = a 2 + b 2
Từ đó suy ra các kết quả.

Với a = -7 và b = 4. Ta có:
a2+2.a.b + b2 = (-7)2+ 2.(-7).4 + 42 = 49 – 56 + 16 = 9
(a + b). (a + b) = [(-7) + 4].[(-7) + 4] = (-3).(-3) = 9

Ta có: \(2\left(a^2+b^2\right)=\left(a+b\right)^2\)
\(\Leftrightarrow2a^2+2b^2-a^2-2ab-b^2=0\)
\(\Leftrightarrow a^2-2ab+b^2=0\)
\(\Leftrightarrow\left(a-b\right)^2=0\)
\(\Leftrightarrow a-b=0\)
hay a=b
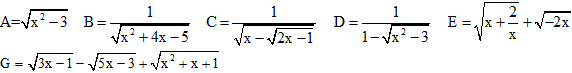 Mn giúp em với ;-;
Mn giúp em với ;-;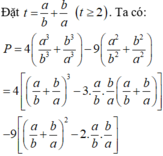
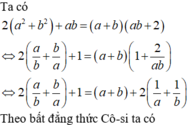
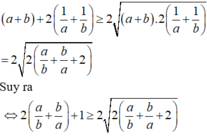
\(\left(a+b\right)^2=\left(a+b\right)\left(a+b\right)=a\times\left(a+b\right)+b\times\left(a+b\right)=a^2+ab+ab+b^2\)
\(=a^2+2ab+b^2\)
\(\Rightarrow\left(a+b\right)^2=a^2+ab+b^2\)
\(\left(a-b\right)^2=\left(a-b\right)\left(a-b\right)=a\left(a-b\right)-b\left(a-b\right)=a^2-ab-ab+b^2\)
\(=a^2-2ab+b^2\)
\(\left(a-b\right)^2=a^2-2ab+b^2\)
(a+b)2=(a+b).(a+b)=a.(a+b)+b.(a+b) =a.a+a.b+a.b+b.b mà a.a=a2;a.b+a.b =2.a.b;b.b=b2suy ra (a+b)2=a2+2.a.b+b2 (đpcm).(a-b)2=(a-b)(a-b)=[a(a-b)]-[b(a-b)] =(a.a-a.b)-(a.b-b.b)=a.a-a.b-a.b+b.b =a.a-(a.b+a.b)+b.b mà a.a=a2; a.b+a.b=2.a.b ; b.b=b2 suy ra : (a-b)2 = a2-2.a.b+b2 (đpcm)