xét các số thực dương a,b thỏa mãn a+b=2 . tìm Max của biểu thức P=a2b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XN
1
AH
Akai Haruma
Giáo viên
14 tháng 11 2021
Lời giải:
Áp dụng BĐT Cô-si:
\(2=a+b=\frac{a}{2}+\frac{a}{2}+b\geq 3\sqrt[3]{\frac{a^2b}{4}}\)
\(\Rightarrow \frac{2}{3}\geq \sqrt[3]{\frac{a^2b}{4}}\Rightarrow \frac{8}{27}\geq \frac{a^2b}{4}\)
\(\Leftrightarrow a^2b\leq \frac{32}{27}\Leftrightarrow P\leq \frac{32}{27}\)
Vậy $P_{\max}=\frac{32}{27}$. Giá trị này đạt tại $\frac{a}{2}=b=\frac{2}{3}$
13 tháng 1 2019
Ta có : \(a^2+b^2+c^2\ge ab+ac+\)\(bc\)(1)
vì , ta có
(1) \(\Leftrightarrow\)\(2\left(a^2+b^2+c^2\right)\)\(\ge2\left(ab+ac+bc\right)\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)\)\(+\left(a^2-2ac+c^2\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\)(luôn đúng) => bất đẳng thức
Ta có :
\(a^2+b^2+c^2-2abc\ge ab+bc+ac-2abc\)
<=>\(a^2+b^2+c^2+2abc-3abc\ge ab+bc+ac-2abc\)
<=> \(1-3abc\ge ab+bc+ac-2abc\)
=> MAX P=1 <=> \(\hept{\begin{cases}a=0\\b=c=1\end{cases}}\)hoặc \(\hept{\begin{cases}b=0\\a=c=1\end{cases}}\)
hoặc \(\hept{\begin{cases}c=0\\a=b=1\end{cases}}\)
Sai thì bảo mình nhé
13 tháng 1 2019
xin lỗi Dòng thứ 8 và 9 phải là
\(a^2+b^2+c^2+2abc-4abc\ge ab+ac+bc-2abc\)
\(\Leftrightarrow1-4abc\ge ab+ac+bc-2abc\)
12 tháng 2 2022
Do \(0\le a,b,c\le1\)
nên\(\left\{{}\begin{matrix}\left(a^2-1\right)\left(b-1\right)\ge0\\\left(b^2-1\right)\left(c-1\right)\ge0\\\left(c^2-1\right)\left(a-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b-b-a^2+1\ge0\\b^2c-c-b^2+1\ge0\\c^2a-a-c^2+1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2b\ge a^2+b-1\\b^2c\ge b^2+c-1\\c^2a\ge c^2+a-1\end{matrix}\right.\)
Ta cũng có:
\(2\left(a^3+b^3+c^3\right)\le a^2+b+b^2+c+c^2+a\)
Do đó \(T=2\left(a^3+b^3+c^3\right)-\left(a^2b+b^2c+c^2a\right)\)
\(\le a^2+b+b^2+c+c^2+a\)\(-\left(a^2+b-1+b^2+c-1+c^2+a-1\right)\)
\(=3\)
Vậy GTLN của T=3, đạt được chẳng hạn khi \(a=1;b=0;c=1\)
15 tháng 2 2016
Ch0 a>0 và n là 1 số tự nhiên
Chứng minh rằng an+1an−2⩾n2(a+1a−2)
Lời giải:
Bất đẳng thức tương đương với (an−1+an−2+...+a+1)≥n2an−1 (hiển nhiên theo AM-GM)
Cách khác:
Do tính đối xứng giữa a và 1a nên ta có thể giả sử a ≥ 1. đặt √a =x ≥ 1.bdt ⇔ x2n+1x2n−2≥n2(x2+1x2−2)⇔(xn−1xn)2≥n2(x−1x)2⇔x^{n}-\frac{1}{x^{n}}\geq n(x-\frac{1}{x})$①.
Với x=1 thì ① đúng
Với x>1 thì ① ⇔xn−1+xn−3...+1xn−3+1xn−1≥n (đúng vì theo bđt AM-GM).
Dấu bằng xảy ra khi x=1 ⇔a=1
18 tháng 5 2023
Ta thấy \(ab\le\dfrac{a^2+b^2}{2}=1\) và \(a+b\le\sqrt{2\left(a^2+b^2\right)}=2\). Áp dụng BĐT B.C.S, ta được \(P=\dfrac{a^4}{ba^2+a^2}+\dfrac{b^4}{ab^2+b^2}\) \(\ge\dfrac{\left(a^2+b^2\right)^2}{ba^2+ab^2+a^2+b^2}=\dfrac{2^2}{ab\left(a+b\right)+2}\ge\dfrac{4}{1.2+2}=1\)
ĐTXR \(\Leftrightarrow a=b=1\)
Vậy GTNN của P là 1 khi \(a=b=1\)
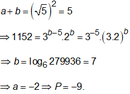
Không có max nhé bạn
Chỗ bbt lấy tới số 2 thôi nhé. Max là 32/27 (khi a=4/3; b=2/3 và hoán vị)