CHO ĐOẠN THẲNG LÀ A= 22014cm. GỌI C1; C2;C3...;C2014 LÀ TRUNG ĐIỂM CỦA AB; AC1;AC2;...;AC2013. TÍNH ĐỘ DÀI ĐOẠN THẲNG C1C2014?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau khi vẽ ta được hình như sau:
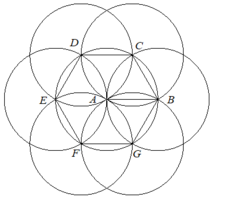
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).

Sau khi vẽ ta được hình bs.17
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).

a) Vì AN+AM= MN
\(\Rightarrow AN=MN-AM=5-3=2\left(cm\right)\)
b) VÌ O là trung điểm nên
\(\Rightarrow OA=ON=\dfrac{AN}{2}=\dfrac{2}{2}=1\left(cm\right)\)
Vì MO= AM+AO
\(\Rightarrow MO=3+1=4\left(cm\right)\)

1: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>DA\(\perp\)DB tại D
=>BD\(\perp\)AM tại D
Ta có: \(\widehat{DAB}+\widehat{DBA}=90^0\)(ΔDBA vuông tại D)
\(\widehat{DBA}+\widehat{DBM}=\widehat{MBA}=90^0\)
Do đó: \(\widehat{DBM}=\widehat{DAB}=35^0\)
Xét (O) có
\(\widehat{DAB}\) là góc nội tiếp chắn cung DB
Do đó: \(\widehat{DOB}=2\cdot\widehat{DAB}=70^0\)
2: Ta có: ΔOAD cân tại O
mà OE là đường trung tuyến
nên OE\(\perp\)AD
Xét tứ giác MBOE có \(\widehat{MBO}+\widehat{MEO}=90^0+90^0=180^0\)
nên MBOE là tứ giác nội tiếp
3: Xét ΔABM vuông tại B có BD là đường cao
nên \(AD\cdot AM=AB^2\)
=>\(AD\cdot AM=\left(2R\right)^2=4R^2\)

giải giúp mình đi mà . Thứ 2 mình đi học rồi . Ai làm xong nhanh nhất mình k cho