Cho tam giác ABC vuông tại A . Có AB=AC . Qua A kẻ đường thẳng xy sao cho B,C nằm cùng phía vs xy . Kẻ BD và CE vuông góc vs xy CM rằng : a, DE = BD + CE
b, gọi M là trung điểm của BC . Lấy N là 1 điểm trên đoạn MC . Kẻ BP và CQ vuông góc vs AN . CM PQ = BP - CQ

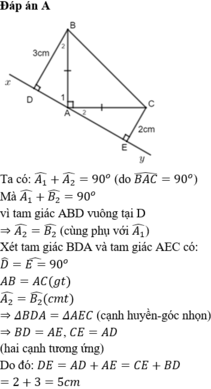
Xét \(\Delta BAD\)và \(\Delta AEC\) có :
\(\widehat{BDA}=\widehat{AEC}\left(=90^o\right)\)
AB = AC ( gt)
\(\widehat{BAD}=\widehat{AEC}\)( cùng phụ với góc EAC)
suy ra \(\Delta ABD=\Delta AEC\)( cạnh huyền góc nhọN)