cho góc aob=100 độ ot là phân giác aob vẽ góc a'ot' đối đỉnh vs aot. so sánh bot' và boa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

12 tháng 7 2018
a) a a' O t t'
b) ta có: góc aOt tù, góc a'Ot' nhọn
=> góc aOt > góc a'Ot'
=> góc aOt và góc a'Ot' không là cặp góc đối đỉnh ( định lí)
30 tháng 9 2021
thích Dứcd ưu tũ 4fd4ss44sdd4đ44đ444đ44d444d44rdrdrdrdrrrrrrfrrttffrfr

VT
4 tháng 9 2017
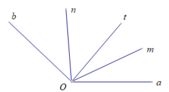
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)

5 tháng 9 2021
a: \(\widehat{a'Ob}+\widehat{aOb}=180^0\)
nên \(\widehat{a'Ob}=130^0\)
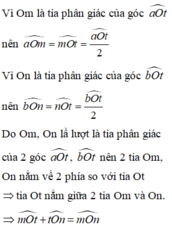
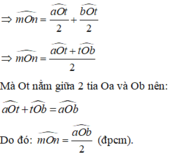
A t B O a' t'
Bài làm
Vì Ot là tia phân giác của \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOt}=\widehat{tOB}=\frac{\widehat{AOB}}{2}=\frac{100^0}{2}=50^0\)
Vì \(\widehat{A'Ot'}\) đối đỉnh với \(\widehat{AOt}\)
=>\(\widehat{A'Ot'}=50^0\)
Ta có: \(\widehat{tOB}+\widehat{BOA'}+\widehat{A'Ot'}=180^0\)( Vì \(\widehat{DOt'}\)là góc bẹp )
Hay \(50^0+\widehat{BOA'}+50^0=180^0\)
\(\Rightarrow\widehat{BOA'}=80^0\)
Lại có: \(\widehat{BOA'}+\widehat{A'Ot'}=80^0+50^0=130^0\)
Hay \(\widehat{BOt'}=130^0\)
Mà \(\widehat{AOB}=100^0\)
=> \(\widehat{BOt'}>\widehat{AOB}\left(130^0>100^0\right)\)
Vậy \(\widehat{BOt'}>\widehat{AOB}\)
# Học tốt #
Bài làm
Vì Ot là tia phân giác của \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOt}=\widehat{tOB}=\frac{\widehat{AOB}}{2}=\frac{100^0}{2}=50^0\)
Vì \(\widehat{A'Ot'}\) đối đỉnh với \(\widehat{AOt}\)
=>\(\widehat{A'Ot'}=50^0\)
Ta có: \(\widehat{tOB}+\widehat{BOA'}+\widehat{A'Ot'}=180^0\)( Vì \(\widehat{DOt'}\)là góc bẹp )
Hay \(50^0+\widehat{BOA'}+50^0=180^0\)
\(\Rightarrow\widehat{BOA'}=80^0\)
Lại có: \(\widehat{BOA'}+\widehat{A'Ot'}=80^0+50^0=130^0\)
Hay \(\widehat{BOt'}=130^0\)
Mà \(\widehat{AOB}=100^0\)
=> \(\widehat{BOt'}>\widehat{AOB}\left(130^0>100^0\right)\)
Vậy \(\widehat{BOt'}>\widehat{AOB}\)
# Học tốt #