x2+mx+m2-3=0
Tìm m để phương trình có 2 nghiệm pb x1,x2 sao cho: x1-3x1x2-m(x2-9)=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 8 2017
Phương trình x 2 – 2(m + 4)x + m 2 – 8 = 0 có a = 1 ≠ 0 và
∆ ' = ( m + 4 ) 2 – ( m 2 – 8 ) = 8 m + 24
Phương trình có hai x 1 ; x 2 ⇔ ∆ ' ≥ 0 ⇔ 8 m + 24 ≥ 0
Áp dụng định lý Vi – ét ta có x 1 + x 2 = 2 ( m + 4 ) ; x 1 . x 2 = m 2 – 8
Ta có:
A = x 1 + x 2 − 3 x 1 x 2
= 2 (m + 4) – 3 ( m 2 – 8) = 3 m 2 + 2m + 32 = − 3 m 2 − 2 3 m − 32 3
= − 3 m − 1 3 2 + 97 3
Nhận thấy A ≤ 97 3 và dấu “=” xảy ra khi m − 1 3 = 0 ⇔ m = 1 3 (TM)
Vậy giá trị lớn nhất của A là 97 3 khi m = 1 3
Đáp án: A
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2022
\(ac=-m^2-1< 0;\forall m\Rightarrow\) phương trình luôn có 2 nghiệm trái dấu với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-m^2-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow m^2-2\left(-m^2-1\right)=3\)
\(\Leftrightarrow3m^2=1\)
\(\Leftrightarrow m^2=\dfrac{1}{3}\)
\(\Leftrightarrow m=\pm\dfrac{1}{\sqrt{3}}\)
LA
21 tháng 4 2022
xét delta
m2 + 4m2 + 4 = 5m2 + 4 > 0
=> phương trình luôn có 2 nghiệm x1x2
theo Vi-ét ta có:
\(\left\{{}\begin{matrix}x1+x2=m\\x1x2=-m^2-1\end{matrix}\right.\)
x12 + x22 = 3
<=> ( x1 +x2 )2 - 2x1x2 = 3
<=> m2 + 2m2 + 2 = 3
<=> 3m2 = 1
=> m2 = \(\dfrac{1}{3}\)
=> m = +- \(\dfrac{1}{\sqrt{3}}\)
2 tháng 7 2023
a: Th1: m=0
=>-2x-1=0
=>x=-1/2
=>NHận
TH2: m<>0
Δ=(-2)^2-4m(m-1)=-4m^2+4m+4
Để phương trình có nghiệm duy nhất thì -4m^2+4m+4=0
=>\(m=\dfrac{1\pm\sqrt{5}}{2}\)
b: Để PT có hai nghiệm phân biệt thì -4m^2+4m+4>0
=>\(\dfrac{1-\sqrt{5}}{2}< m< \dfrac{1+\sqrt{5}}{2}\)
CM
22 tháng 7 2017
Phương trình có hai nghiệm
B = 2 ( x 1 2 + x 2 2 ) + 16 − 3 x 1 x 2
= 2 ( x 1 + x 2 ) 2 − 4 x 1 x 2 + 16 − 3 x 1 x 2 = 2 ( 2 m + 2 ) 2 − 4 ( m 2 + 2 ) + 16 − 3 ( m 2 + 2 ) = 4 m 2 + 16 m + 16 − 3 ( m 2 + 2 ) = 2 m + 4 − 3 ( m 2 + 2 ) = − 3 m 2 + 2 m − 2
Xét hàm số y = − 3 m 2 + 2 m − 2 với m ≥ 1 2
Bảng biến thiên
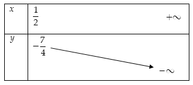
Suy ra giá trị m a x m ≥ 1 2 y = − 7 4 khi m = 1 2
Vậy giá trị lớn nhất của biểu thức B là - 7 4 khi m = 1 2
Đáp án cần chọn là: B
28 tháng 5 2023
a: Δ=(m+1)^2-4m=(m-1)^2>=0
=>Phương trình luôn có nghiệm
b: x1^2+x2^2+3x1x2=5
=>(x1+x2)^2+x1x2=5
=>(m+1)^2+m=5
=>m^2+3m-4=0
=>(m+4)(m-1)=0
=>m=1 hoặc m=-4
31 tháng 3 2023
x1+x2=2m+2; x1x2=m^2+4
x1^2+2(m+1)x2<=2m^2+20
=>x1^2+x2(x1+x2)<=2m^2+20
=>x1^2+x2x1+x2^2<=2m^2+20
=>(x1+x2)^2-x1x2<=2m^2+20
=>(2m+2)^2-(m^2+4)<=2m^2+20
=>4m^2+8m+4-m^2-4-2m^2-20<=0
=>m^2-8m-20<=0
=>m<=-10 hoặc m>2
LD
31 tháng 3 2023
\(x^2-2\left(m+1\right)x+m^2+4=0\left(1\right)\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta'>0\) hay \(\Delta'=\left(m+1\right)^2-m^2-4=m^2+2m+1-m^2-4=2m-4>0\Leftrightarrow m>2\)
Theo hệ thức Viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=m^2+4\end{matrix}\right.\)
Vì \(x_1^2\) là nghiệm của phương trình (1) nên ta có : \(x_1^2-2\left(m+1\right)x+m^2+4=0\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta lại có : \(x_1^2+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2\le2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-m^2-4\le2m^2+20\)
\(\Leftrightarrow4\left(m+1\right)^2-m^2\le2m^2+20\)
\(\Leftrightarrow4\left(m^2+2m+1\right)-m^2\le2m^2+20\)
\(\Leftrightarrow m^2+8m-16\le0\)
\(\Leftrightarrow-10\le m\le2\)
Kết hợp điều kiện....
TA
4 tháng 6 2021
PT có 2 nghiệm phân biệt `<=> \Delta'>0`
`<=>m^2-(m^2+m-5)>0`
`<=>-m+5>0`
`<=> m < 5`
Viet: `x_1+x_2=2m`
`x_1x_2=m^2+m-5`
Theo đề bài: `2(x_1^2+x_2^2)-3x_1x_2=29`
`<=>2[(x_1+x_2)^2-2x_1x_2]-3x_1x_2=29`
`<=>2(x_1+x_2)^2-7x_1x_2=29`
`<=>2.4m^2 - 7(m^2+m-5)=29`
`<=>` \(\left[{}\begin{matrix}m=6\left(L\right)\\m=1\left(TM\right)\end{matrix}\right.\)
Vậy `m=1`.
Sorry sai đề đề đúng là ntn x1-3x1x2-m(x2+9)=0