Cho tam giác ABC có 2 đường trung tuyến AD và BE vuông góc với nhau. Chứng minh rằng BC < 2AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
20 tháng 6 2019
A B C D E G 1 1 1
BC < 2AC nếu \(\frac{1}{2}BC=CD< AC\)
Xét hai tam giác ADC có \(\widehat{D_1}=\widehat{G_1}+\widehat{B_1}\).Theo giả thiết \(\widehat{G_1}=90^0\)nên \(\widehat{D_1}\)là góc tù .
Cạnh AC đối diện với \(\widehat{D_1}\) nên là cạnh lớn nhất , Vậy \(AC>DC\)hay \(2AC>2DC=BC\)
CM
23 tháng 12 2019
Gọi giao điểm của hai đường thẳng AD và BE là G.
+) Xét tam giác BDG có góc ∠D1 là góc ngoài tam giác nên :
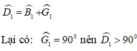
+)Xét tam giác ADC có ∠D1 + ∠A + ∠C = 180º mà ∠D1 > 90º nên ∠D1 là góc lớn nhất trong tam giác đó:
Suy ra: ∠D1 > ∠A
Suy ra: AC > CD ( cạnh đối diện với góc lớn hơn thì lớn hơn ). (1)
+) Mà D là trung điểm của BC nên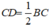 
(2)
Từ (1) và (2) suy ra: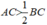 
hay 2AC > BC ( điều phải chứng minh )
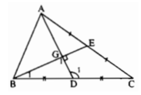
A E G B D C 1 1 1
BC < 2AC nếu \(\frac{1}{2}\)BC = CD < AC
Xét hai tam giác ADC có \(\widehat{D_1}\)=\(\widehat{G_1}\)+\(\widehat{B_1}\).Theo giả thiết \(\widehat{G_1}\)=\(90^o\)nên \(\widehat{D_1}\)là góc tù.
Cạnh AC đối diện với \(\widehat{D_1}\)nên là cạnh lớn nhất. Vậy AC > DC hay 2AC > 2DC = BC