Phương trình : \(4sin^22x-3sin2xcos2x-cos^22x=0\) có bao nhiêu nghiệm trong khoảng ( \(0;\Pi\) ) ?
A . 1
B . 2
C . 3
D . 4
Trình bày bài giải chi tiết rồi mới chọn đáp án nha các bạn .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
PT $\Leftrightarrow (\sin 2x-\cos 2x)(4\sin 2x+\cos 2x)=0$
$\Rightarrow \sin 2x=\cos 2x$ hoặc $4\sin 2x+\cos 2x=0$
Nếu $\sin 2x=\cos 2x$. Kết hợp với $\sin ^22x+\cos ^22x=1$ suy ra $\sin 2x=\cos 2x=\frac{\pm}{\sqrt{2}}$
$\Rightarrow x=\frac{\pi}{8}+\frac{k\pi}{2}$ với $k$ nguyên
Vì $x\in (0;\pi)$ nên $x=\frac{\pi}{8}$ hoặc $x=\frac{5\pi}{8}$
Nếu $4\sin 2x+\cos 2x=0$
$\Rightarrow \tan 2x=\frac{-1}{4}$
$\Rightarrow x=\frac{1}{2}k\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4}$
Vì $x\in (0;\pi)$ nên $x=\frac{1}{2}\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4};\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4}$
Vậy có $4$ nghiệm thỏa mãn.
Lời giải:
PT $\Leftrightarrow (\sin 2x-\cos 2x)(4\sin 2x+\cos 2x)=0$
$\Rightarrow \sin 2x=\cos 2x$ hoặc $4\sin 2x+\cos 2x=0$
Nếu $\sin 2x=\cos 2x$. Kết hợp với $\sin ^22x+\cos ^22x=1$ suy ra $\sin 2x=\cos 2x=\frac{\pm}{\sqrt{2}}$
$\Rightarrow x=\frac{\pi}{8}+\frac{k\pi}{2}$ với $k$ nguyên
Vì $x\in (0;\pi)$ nên $x=\frac{\pi}{8}$ hoặc $x=\frac{5\pi}{8}$
Nếu $4\sin 2x+\cos 2x=0$
$\Rightarrow \tan 2x=\frac{-1}{4}$
$\Rightarrow x=\frac{1}{2}k\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4}$
Vì $x\in (0;\pi)$ nên $x=\frac{1}{2}\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4};\pi +\frac{1}{2}\tan ^{-1}\frac{-1}{4}$
Vậy có $4$ nghiệm thỏa mãn.

Lời giải:
$2\cos ^22x+5\cos 2x-3=0$
$\Leftrightarrow (2\cos 2x-1)(\cos 2x+3)=0$
$\Leftrightarrow 2\cos 2x-1=0$ (chọn) hoặc $\cos 2x=-3$ (loại)
Vậy $2\cos 2x-1=0$
$\Leftrightarrow \cos 2x=\frac{1}{2}$
$\Rightarrow x=\frac{\pm \pi}{3}+2k\pi$ với $k$ nguyên
Để nghiệm trong khoảng $(0;2\pi)$ thì $k=0$ với họ nghiệm $(1)$ và $k=1$ với họ nghiệm $(2)$
Vậy nghiệm của pt thỏa đề là:
$x=\frac{\pi}{3}; x=\frac{5}{3}\pi$
Tổng nghiệm: $\frac{\pi}{3}+\frac{5\pi}{3}=2\pi$

Đáp án A
Dùng công thức ![]() để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
để đưa phương trình ban đầu về đa thức bậc 2 theo sin x.
Giải phương trình này tìm x và đối chiếu với yêu cầu ![]() để tìm được giá trị của x.
để tìm được giá trị của x.
Ta có
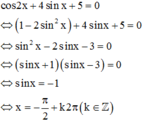
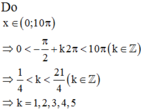
Do đó tập nghiệm của phương trình đã cho trên 0 ; 10 π là
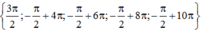

1a.
Đặt \(5x+6=u\)
\(cos2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow1-2sin^2u+4\sqrt{2}sinu-4=0\)
\(\Leftrightarrow2sin^2u-4\sqrt{2}sinu+3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=\dfrac{3\sqrt{2}}{2}>1\left(loại\right)\\sinu=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Rightarrow sin\left(5x+6\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+6=\dfrac{\pi}{4}+k2\pi\\5x+6=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{6}{5}+\dfrac{\pi}{20}+\dfrac{k2\pi}{5}\\x=-\dfrac{6}{5}+\dfrac{3\pi}{20}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
1b.
Đặt \(2x+1=u\)
\(cos2u+3sinu=2\)
\(\Leftrightarrow1-2sin^2u+3sinu=2\)
\(\Leftrightarrow2sin^2u-3sinu+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinu=1\\sinu=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(2x+1\right)=1\\sin\left(2x+1\right)=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\dfrac{\pi}{2}+k2\pi\\2x+1=\dfrac{\pi}{6}+k2\pi\\2x+1=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}+\dfrac{\pi}{4}+k\pi\\x=-\dfrac{1}{2}+\dfrac{\pi}{12}+k\pi\\x=-\dfrac{1}{2}+\dfrac{5\pi}{12}+k\pi\end{matrix}\right.\)